四轴飞行器姿态解算介绍
一.姿态的描述方法
四元数
因为网络上的欧拉角的文章讲解的也比较详细了,所以这里直接开始介绍四元数。基本定义 顾名思义四元数就是由四个元构成的数: \[\textbf{Q}(q_0+q_1+q_2+q_3)=q_0+q_1 \textbf{i} +q_2 \textbf{j} +q_3 \textbf{k} \]
其中\(q_0\)、\(q_1\)、\(q_2\)、\(q_3\)是实数,\(\textbf{i}\)、\(\textbf{j}\)、\(\textbf{k}\) 是互相正交的单位向量,又是虚单位\(\sqrt{-1}\),具体规定的四元数乘法为: \[\begin{align}\textbf{i} \bigotimes \textbf{i} &=-1,\quad \textbf{j}\bigotimes \textbf{j} =-1,\quad \textbf{k} \bigotimes \textbf{k} =-1 \quad \\ \textbf{i} \bigotimes \textbf{j} &= \textbf{k} ,\ \quad \textbf{j} \bigotimes \textbf{k} = \textbf{i} ,\ \quad \textbf{k} \bigotimes i= \textbf{j} \quad \\ \textbf{j} \bigotimes \textbf{i} &=- \textbf{k} ,\quad \textbf{k} \bigotimes \textbf{j} =- \textbf{i} ,\quad \textbf{i} \bigotimes \textbf{k} =- \textbf{j} \quad \end{align} \]表达方式
- 矢量式 \[\textbf{Q}=q_0+\textbf{q}\]
- 复数式 \[\textbf{Q}=q_0+q_1\textbf{i}+q_2 \textbf{j} +q_3 \textbf{k}\] 记\(Q\)的共轭复数为\(Q^*\) \[\textbf{Q*}=q_0-q_1\textbf{i}-q_2 \textbf{j} -q_3 \textbf{k}\]
- 矩阵式 \[\textbf{Q}=\begin{bmatrix} q_0\\q_1\\q_2\\q_3 \end{bmatrix}\]
四元数大小 \[||\textbf{Q}||=q_0^2+q_1^2+q_2^2+q_3^2\]
四元数运算
- 加法 设: \[\textbf{Q}=q_0+q_1 \textbf{i} +q_2 \textbf{j} +q_3 \textbf{k}\\ \textbf{P}=p_0+p_1 \textbf{i} +p_2 \textbf{j} +p_3 \textbf{k}\] 则: \[\textbf{Q}\pm\textbf{P}=(q_0\pm p_0)+(q_1\pm p_1) \textbf{i} +(q_2\pm p_2) \textbf{j} +(q_3\pm p_3) \textbf{k}\]
- 乘法 \[\begin{align} \textbf{P}\bigotimes \textbf{Q}& =(\textbf{P}=p_0+p_1 \textbf{i} +p_2 \textbf{j} +p_3 \textbf{k})\bigotimes (q_0+q_1 \textbf{i} +q_2 \textbf{j} +q_3 \textbf{k})\\ &=(p_0q_0-p_1q_1-p_2q_2-p_3q_3)+(p_0q_1+p_1q_0+p_2q_3-p_3q_2)\textbf{i}\\ &+(p_0q_2+p_2q_0+p_3q_1-p_1q_3)\textbf{j}+(p_0q_3+p_3q_0+p_1q_2-p_2q_1)\textbf{k}\\ &=r_0+r_1\textbf{i}+r_2\textbf{j}+r_3\textbf{k} \end{align}\] 乘法即简单的系数相乘。 当然也可以写成矩阵形式: \[\begin{bmatrix} r_0 \\ r_1 \\r_2 \\r_3\end{bmatrix}= \begin{gather*}\begin{bmatrix} & p_0 \ &-p_1 \ &-p_2 \ &-p_3\\ & p_1 \ &p_0 \ &-p_3 \ &p_2\\ & p_2 \ &p_3 \ &p_0 \ &-p_1\\ & p_3 \ &-p_2 \ &p_1 \ &p_0\\ \end{bmatrix}\end{gather*}\begin{bmatrix}q_0\\q_1\\q_2\\q_3\end{bmatrix} \] 要注意: \[\textbf{P}\bigotimes\textbf{Q}\neq\textbf{Q}\bigotimes\textbf{P}\] 四元数的乘法也满足分配律和结合律 \[\textbf{P}\bigotimes(\textbf{Q}+\textbf{R})=\textbf{P}\bigotimes\textbf{Q}+\textbf{P}\bigotimes\textbf{R}\]
四元数与姿态阵的关系
设有参考坐标系\(R\),坐标轴为\(x_0,y_0,z_0\),坐标轴方向的单位向量为\(\textbf{i}_0,\textbf{j}_0,\textbf{k}_0\)。刚体相对\(R\)系做定点转动,定点为\(O\)。取坐标系\(b\)与刚体固联,\(b\)系的坐标轴为\(x,y,z\),坐标方向的单位向量为\(\textbf{i},\textbf{j},\textbf{k}\)。假设初始状态下\(b\)系与\(R\)系重合。为了便于分析刚体的空间角位置,在刚体上取一点\(A\),转动点为点\(O\)。如下图所示:
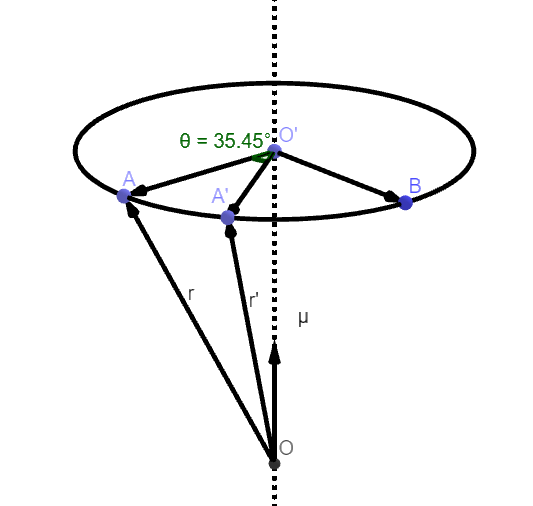
设刚体以\(\boldsymbol{\omega}=\omega_x\textbf{i}+\omega_y\textbf{j}+\omega_z\textbf{k}\)相对于\(\textbf{R}\)系旋转,初始时刻位置向量为\(\textbf{OA}=\textbf{r}\),经过时间\(t\)后位置向量处于\(\mathop{\textbf{OA}'}=\mathop{\textbf{r}'}\)。根据欧拉定理,仅考虑刚体在0时刻和\(t\)时刻的角位置时,刚体从\(\mathop{\textbf{A}}\)位置转动到\(\mathop{\textbf{A}'}\)可等效成绕瞬轴\(\mu\)(单位向量)转过\(\theta\)角一次完成。这样,单位向量做圆锥运动,\(\mathop{\textbf{A}}\)和\(\mathop{\textbf{A}'}\)位于同一个圆上,\(\mathop{\textbf{r}}\)和\(\mathop{\textbf{r}'}\)位于同一圆锥面上。
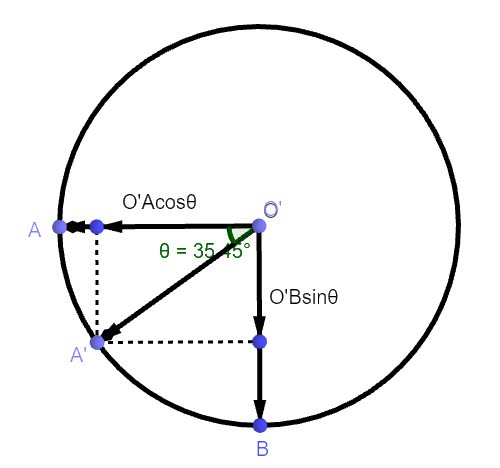
下面分析\(\mathop{\textbf{r}}\)和\(\mathop{\textbf{r}'}\)的关系。在圆上取一点\(B\),使\(\angle A\mathop{O'}B=90^\circ\),由图得:
\[ \begin{align} \mathop{\boldsymbol{O}\boldsymbol{O}'} &=(\boldsymbol{r}\cdot\boldsymbol{u})\boldsymbol{u} \\ \mathop{\boldsymbol{O}'\boldsymbol{A}} &=\boldsymbol{r}-\mathop{\boldsymbol{O}\boldsymbol{O}'}=\boldsymbol{r}-(\boldsymbol{r}\cdot\boldsymbol{u})\boldsymbol{u} \end{align} \]