我使用的matlab是2017b，但是我在官方查找文档，其中的例子这个版本没有。所以我摸索了一番。使用这个函数的动机是我需要是用libsvm做回归模型的训练，其中训练的优化函数是遗传算法（谢菲尔德工具箱），老的工具箱不支持并行计算以及GPU加速，所以我使用Matlab自带的遗传算法函数进行参数的优化。

利用ga优化非光滑函数

程序

xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);% 构造函数
Z = reshape(Z,size(X));

surf(X,Y,Z,'MeshStyle','none')% 绘图
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')

rng default % 保证再生性
x = ga(@ps_example,2)

结果： 

Optimization terminated: average change in the fitness value less than options.FunctionTolerance.

x =

   -4.6793   -0.0860
函数图像：

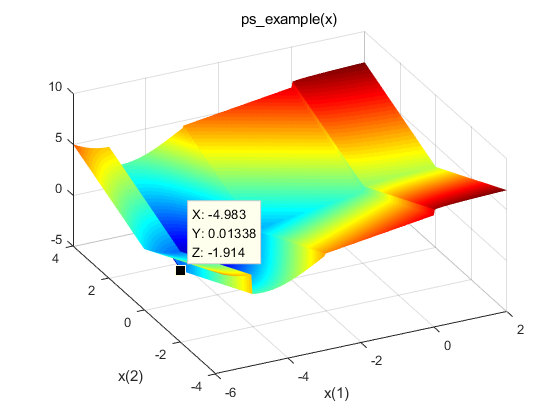
分析

GA函数最基本的用法就是构造一个输入为行向量，输出为数值的函数例如Z = ps_example([X(:),Y(:)])。 接下来使用GA函数的时候，第一个参数是函数句柄，第二个参数是函数参数个数。 返回值则是输出参数函数句柄所使用的参数行向量矩阵。

最小化具有线性约束的非光滑函数

程序

待寻优函数的输入参数是一个行向量，因此传入x(1)代表x，x(2)代表y。 如果需要设置区域范围x + y >= 1和y <= 5 + x的ps_example函数最小化。 首先, 将两个不等式约束转换为矩阵形式A*x <= b。换言之, 获取不等式左侧的x变量, 并使两个不等式小于等于: 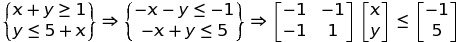那么将矩阵乘法的系数作为约束条件：令A = [-1,-1;-1,1]; b = [-1;5];。全程序如下： 

    xi = linspace(-6,2,300);
    yi = linspace(-4,4,300);
    [X,Y] = meshgrid(xi,yi);
    Z = ps_example([X(:),Y(:)]);% 构造函数
    Z = reshape(Z,size(X));
+   A = [-1,-1;% 添加约束
+       -1,1];
+   b = [-1;5];

    surf(X,Y,Z,'MeshStyle','none')% 绘图
    colormap 'jet'
    view(-26,43)
    xlabel('x(1)')
    ylabel('x(2)')
    title('ps\_example(x)')

    rng default; % 再生性
+   x = ga(@ps_example,2,A,b)
结果如下： 
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.

x =

    0.9991   -0.0000
# 总结 为待寻优函数添加约束条件时，需要将其转换为矩阵乘法的形式，再提取出其中的参数。

最小化具有线性等式和不等式约束的非光滑函数

程序

如果添加的约束条件不是小于等于，而是一个小于等于，一个等于。 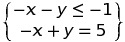那么设置约束条件时就需要分开设置(A对应b,Aeq对应beq): 

A = [-1 -1];
b = -1;
Aeq = [-1 1];
beq = 5;
修改ga函数输入为： 
x = ga(@ps_example,2,A,b,Aeq,beq)
结果： 
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.
x = 1×2

   -2.0000    2.9990
## 结论 小于等于的约束条件和等于的约束条件要分开来写。 # 线性约束和边界优化 ## 程序 保持上一例不变，现在若要约束x,y的取值范围为1 <= x <= 6和-3 <= y <= 8。 那么设置界限lb和ub。 
lb = [1 -3];
ub = [6 8];
修改ga函数为： 
x = ga(@ps_example,2,A,b,Aeq,beq,lb,ub)
结果： 
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.
x = 1×2

    1.0001    5.9992
# 结论 对于输入参数限制的进一步深入。

利用ga优化非线性约束

程序

如果约束条件改为非线性的函数：\(2x^2+y^2\le3\)和\((x^2+1)^2=(\frac{y}{2})^4\)。 那么首先先将非线性的约束条件写成函数的形式： 1. 新建函数ellipsecons.m 

function [c,ceq] = ellipsecons(x)

c = 2*x(1)^2 + x(2)^2 - 3;
ceq = (x(1)+1)^2 - (x(2)/2)^4;
end
1. 修改原程序为： 
xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);% 构造函数
Z = reshape(Z,size(X));

surf(X,Y,Z,'MeshStyle','none')% 绘图
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')

rng default; % 再生性
x = ga(@ps_example,2,[],[],[],[],[],[],@ellipsecons)
结果：

Optimization terminated: average change in the fitness value less than options.FunctionTolerance
 and constraint violation is less than options.ConstraintTolerance.

x =

   -0.9766    0.0362

结论

前面四个空矩阵都是ps_example的约束条件，约束条件函数ellipsecons的约束条件是后面两个空矩阵。 # 使用非默认选项最小化 ## 程序 为了获得更精确的解决方案, 可以将约束公差设置为1e-6。并监视规划求解进度, 设置一个绘图函数。 总程序如下： 

close all
clear
xi = linspace(-6,2,300);
yi = linspace(-4,4,300);
[X,Y] = meshgrid(xi,yi);
Z = ps_example([X(:),Y(:)]);% 构造函数
Z = reshape(Z,size(X));

A = [-1 -1];%添加约束
b = -1;
Aeq = [-1 1];
beq = 5;

surf(X,Y,Z,'MeshStyle','none')% 绘图
colormap 'jet'
view(-26,43)
xlabel('x(1)')
ylabel('x(2)')
title('ps\_example(x)')


options = optimoptions('ga','ConstraintTolerance',1e-6,'PlotFcn', @gaplotbestf);%设置选项
rng default; % 再生性
x = ga(@ps_example,2,A,b,Aeq,beq,[],[],[],options)
结果： 
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.

x =

   -2.0000    3.0000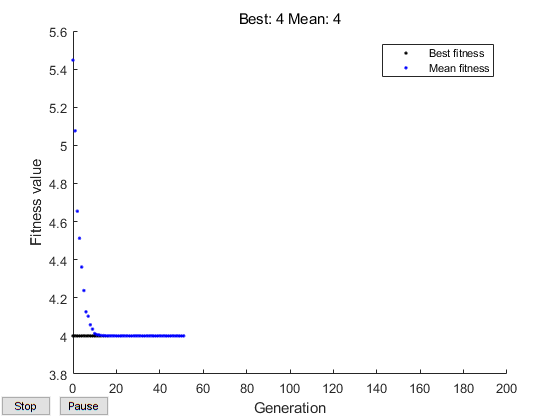
# 实例：优化libsvm训练模型 很难受，我尝试改写了程序，但是并不能使用并行加速，还是很慢。。接下来我要找别的方式去加速。