#include <cmath>
#include <fstream>
#include <iostream>
#include <set>
#include <stack>
#include <vector>
using namespace std;
#define Dcout(x) cout << #x << ": " << (x) << endl
struct Node {
double x, y;
int pts, cluster;
bool visited= false;
vector<int> contains;
enum { Core= 0, Border= 1, Noise= 2 } tag;
Node() : x(0), y(0), pts(1), cluster(0), tag(Noise) {}
Node(double a, double b) : x(a), y(b), pts(1), cluster(-1), tag(Noise) {}
Node(double a, double b, int c)
: x(a), y(b), pts(1), cluster(c), tag(Noise) {}
};
class DBSCAN {
public:
vector<set<int> *> cluster;
vector<Node> a_node;
vector<Node *> c_node;
DBSCAN(double eps, int minpts, vector<struct Node> &l)
: _eps(eps), _minpts(minpts) {
_total= l.size();
a_node= l;
dis= new double *[_total];
for (int i= 0; i < _total; ++i) { dis[i]= new double[_total]; }
}
~DBSCAN() { delete[] dis; }
void FindCore(void) {
for (int i= 0; i < _total; ++i) {
for (int j= i + 1; j < _total; ++j) {
dis[i][j]= EuclideanDis(a_node[i], a_node[j]);
if (dis[i][j] <= _eps) {
a_node[i].pts++;
a_node[j].pts++;
}
}
}
for (int i= 0; i < _total; ++i) {
if (a_node[i].pts >= _minpts) {
a_node[i].tag= Node::Core;
c_node.push_back(&a_node[i]);
}
}
}
void ConnectCore(void) {
for (int i= 0; i < c_node.size(); ++i) {
for (int j= i + 1; j < c_node.size(); ++j) {
if (EuclideanDis(*c_node[i], *c_node[j]) < _eps) {
c_node[i]->contains.push_back(j);
c_node[j]->contains.push_back(i);
}
}
}
}
void DFSCore(void) {
int cnt= -1;
for (int i= 0; i < c_node.size(); i++) {
stack<Node *> ps;
if (c_node[i]->visited) continue;
++cnt;
a_node[c_node[i]->cluster].cluster= cnt;
ps.push(c_node[i]);
Node *v;
while (!ps.empty()) {
v= ps.top();
v->visited= 1;
ps.pop();
for (int j= 0; j < v->contains.size(); j++) {
if (c_node[v->contains[j]]->visited) continue;
c_node[v->contains[j]]->cluster= cnt;
c_node[v->contains[j]]->visited= true;
ps.push(c_node[v->contains[j]]);
}
}
}
}
void AddBorder(void) {
for (int i= 0; i < _total; ++i) {
if (a_node[i].tag == Node::Core) { continue; }
if (a_node[i].tag == Node::Noise) { a_node[i].cluster= -1; }
for (int j= 0; j < c_node.size(); ++j) {
if (EuclideanDis(a_node[i], *c_node[j]) < _eps) {
a_node[i].tag= Node::Border;
a_node[i].cluster= c_node[j]->cluster;
break;
}
}
}
}
private:
double _eps;
int _total, _minpts;
double **dis;
inline double EuclideanDis(const struct Node &a, const struct Node &b) {
return sqrt(((a.x - b.x) * (a.x - b.x)) + ((a.y - b.y) * (a.y - b.y)));
}
};
int main(int argc, char const *argv[]) {
vector<struct Node> nodes;
ifstream fin("in");
if (!fin) {
return -1;
} else {
int i= -1;
char s[100];
for (double x, y; fin.getline(s, 100);) {
sscanf(s, "%lf,%lf", &x, &y);
nodes.push_back(Node(x, y, ++i));
}
}
DBSCAN dbscan(0.1, 10, nodes);
dbscan.FindCore();
dbscan.ConnectCore();
dbscan.DFSCore();
dbscan.AddBorder();
ofstream fout("out");
if (!fout) {
return -1;
} else {
for (auto &it : dbscan.a_node) {
fout << it.cluster << endl;
}
fout.close();
}
return 0;
}
|
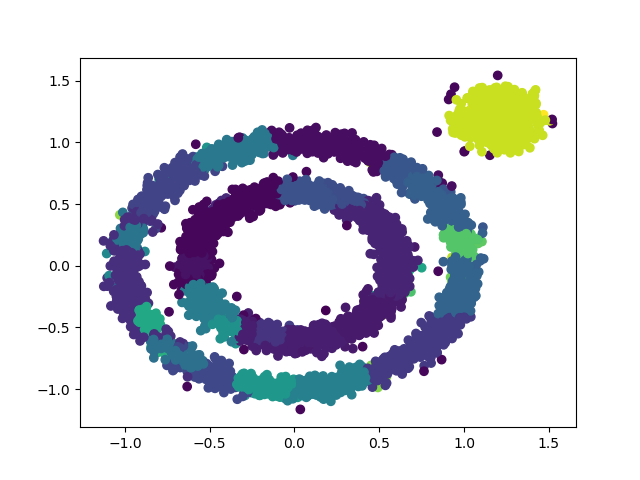 可以发现当前参数被分为多个类。我找了半天才发现,原来是我加入簇中的时候,只循环遍历了所有簇中有没有该元素,但是忽略了一点,有可能此前的两个簇,都是互不相交的。但是到最后的两个元素,另其突然相交了。所以需要修改加入簇的操作。
可以发现当前参数被分为多个类。我找了半天才发现,原来是我加入簇中的时候,只循环遍历了所有簇中有没有该元素,但是忽略了一点,有可能此前的两个簇,都是互不相交的。但是到最后的两个元素,另其突然相交了。所以需要修改加入簇的操作。