这是吴恩达老师的机器学习作业....并不是我们学校的 hh

因为机器学习这个课是老师在2014年讲的,那时候Python还不火,所以老师讲的时候用的是ocatve,现在我准备都用Python写.

总结

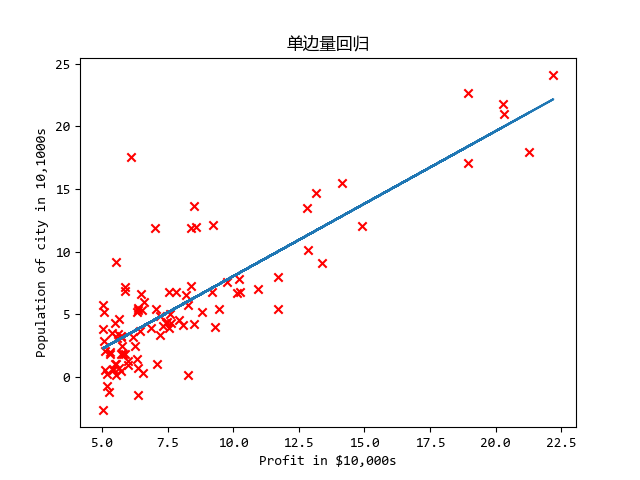
这是第一周作业,单/多变量线性回归

  1. 注意损失函数求导出来的结果,更新方式是不一样的

  2. python中的矩阵和list类型非常蛋疼,不如matlab全是矩阵就好了

  3. 给X加列,可以利用矩阵乘法快速求解

  4. 绘3维图时要用meshgrid函数连接变量

  5. numpy.std函数要加上参数ddof=1，因为他的标准差默认除以n

重要公式的推导

这里有一个多变量的梯度更新，需要把原来的损失函数进行求导，因为现在是每一个变量都是向量，所以推导的时候我纠结了好一会。具体如下：

注：上标为行数，下标为列数，设数据X=[m,n]

\[ \begin{aligned} \theta_j &= \theta_j - \alpha\frac{\partial}{\partial\theta_j}J(\theta) = \theta_j - \alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})*x_j^{(i)} \\ \theta_j &-=\frac{ \alpha}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})*x_j^{(i)} \end{aligned} \] 现在我们分析此部分\(\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})*x_j^{(i)}\)：

注：以下都省略了常数项\(\alpha/m\)

\[ \begin{aligned} \because &x=[m,n]\ \ \ y=[m,1]\\ \therefore &x^{(i)} =[1,n]\ \ \ y^{(i)}=[1,1]\ \ \ \theta=[n,1] \\ \Rightarrow &h_\theta(x^{(i)})=x^{(i)}*\theta=[1,1]\\ \Rightarrow &h_\theta(x^{(i)})-y^{(i)}=[1,1]=E_\theta^{(i)}\\ \because &\sum_{i=1}^{m}(h_\theta(x^{(i)}) - y^{(i)})*x_j^{(i)}=\sum_{i=1}^{m}E_\theta^{(i)}*x_j^{(i)}\\ &=E_\theta^{(0)}*x_j^{(0)}+E_\theta^{(1)}*x_j^{(1)}+\ldots+E_\theta^{(m)}*x_j^{(m)}\\ \therefore \Theta&= \begin{bmatrix} x_1^1E_1 + x_2^1E_1 + \ldots + x_m^1E_1 \\ x_1^2E_2 + x_2^2E_2 + \ldots + x_m^2E_2 \\ x_1^nE_n + x_2^nE_n + \ldots + x_m^nE_n \\ \end{bmatrix} \end{aligned} \]

将其放到全局的矩阵中就是这样：

\[ \begin{aligned} X&=\begin{bmatrix} x_1^1 & x_2^1 & \ldots & x_n^1 \\ \vdots & \vdots & \ldots & \vdots \\ x_1^m & x_2^m & \ldots & x_n^1 \\ \end{bmatrix}\\ Y&=\begin{bmatrix} y_1^1 \\ \vdots \\ y_1^m \\ \end{bmatrix}\\ \theta&=\begin{bmatrix} \theta_1^1 \\ \vdots \\ \theta_1^n \\ \end{bmatrix} \\ \Theta-&=X^T(h_\theta(X) -Y) = X^T(X*\Theta-Y) \\ &= \begin{bmatrix} x_1^1 & x_1^2 & \ldots & x_1^m \\ \vdots & \vdots & \ldots & \vdots \\ x_n^1 & x_n^2 & \ldots & x_n^m \\ \end{bmatrix}* (\begin{bmatrix} x_1^1 & x_2^1 & \ldots & x_n^1 \\ \vdots & \vdots & \ldots & \vdots \\ x_1^m & x_2^m & \ldots & x_n^1 \\ \end{bmatrix}* \begin{bmatrix} \theta_1^1 \\ \vdots \\ \theta_1^n \\ \end{bmatrix}- \begin{bmatrix} y_1^1 \\ \vdots \\ y_1^m \\ \end{bmatrix}) \\ &= \begin{bmatrix} x_1^1 & x_1^2 & \ldots & x_1^m \\ \vdots & \vdots & \ldots & \vdots \\ x_n^1 & x_n^2 & \ldots & x_n^m \\ \end{bmatrix}* \begin{bmatrix} h_1^1 - y_1^1 \\ \vdots \\ h_1^m - y_1^m \\ \end{bmatrix}\\ &= \begin{bmatrix} x_1^1E_1 + x_2^1E_1 + \ldots + x_m^1E_1 \\ x_1^2E_2 + x_2^2E_2 + \ldots + x_m^2E_2 \\ x_1^nE_n + x_2^nE_n + \ldots + x_m^nE_n \\ \end{bmatrix} \end{aligned} \]

即推出：

\[\Theta-=\frac{\alpha}{m}X^T(X*\Theta-Y)\] # 代码

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np


# 加载数据
def load_data(filepath: str)->np.ndarray:
    dataset = []
    f = open(filepath)
    for line in f:
        dataset.append(line.strip().split(','))
    return np.asfarray(dataset)

# 定义推演函数


def h_fuc(x: float, theta: np.ndarray)->float:
    return theta[0, 0]+theta[0, 1]*x


# z定义损失函数
def computeCost(X: np.ndarray, y: np.ndarray, theta: np.ndarray)->float:
    m = y.shape[0]
    return np.sum(np.power(np.dot(X, theta)-y, 2))/(2*m)


# 多参数损失函数计算
def computeCostMulti(X: np.ndarray, y: np.ndarray, theta: np.ndarray)->float:
    m = y.shape[0]
    return np.sum(np.power(np.dot(X, theta)-y, 2))/(2*m)


# 更新参数
def gradientDescent(X: np.ndarray, y: np.ndarray, theta: np.ndarray, alpha: float, num_iters: int):
    m = y.shape[0]
    j_history = np.zeros((num_iters, 1))
    theta_s = theta.copy()
    for i in range(num_iters):
        theta[0, 0] -= alpha / m * np.sum(np.dot(X, theta_s) - y)
        theta[1, 0] -= alpha / m * np.sum((np.dot(X, theta_s) - y)*X)
        # 必须同时更新theta(1)和theta(2)
        theta_s = theta
        j_history[i, 0] = computeCost(X, y, theta)
    return j_history


def gradientDescentMulti(X: np.ndarray, y: np.ndarray, theta: np.ndarray, alpha: float, num_iters: int):
    m = y.shape[0]
    j_history = np.zeros((num_iters, 1))
    for i in range(num_iters):
        theta -= alpha*(X.T@(X@theta-y))/m
        j_history[i, 0] = computeCostMulti(X, y, theta)
    return theta, j_history


def featureNormalize(X: np.ndarray):
    X_norm = X
    mu = np.zeros((1, X.shape[0]))
    sigma = np.zeros((1, X.shape[0]))
    mu = np.mean(X, axis=0)
    # 加上ddof=1 因为matlab中默认除以 n-1 np 默认除以 n
    sigma = np.std(X, axis=0, ddof=1)
    X_norm = (X-mu)/sigma
    return X_norm, mu, sigma


# 正规方程求解
def normalEqn(X: np.ndarray, y: np.ndarray):
    theta = np.linalg.inv(X.T@X)@X.T@y
    return theta


if __name__ == "__main__":

    # 步骤一（替换sans-serif字体）
    plt.rcParams['font.sans-serif'] = ['YaHei Consolas Hybrid']
    # 步骤二（解决坐标轴负数的负号显示问题）
    plt.rcParams['axes.unicode_minus'] = False

    """ 以下为单变量回归 """
    dataset = load_data('machine_learning_exam/week1/ex1data1.txt')
    m = dataset.shape[0]
    # x 添加一列 便于矩阵计算 x=[m,2]
    X = np.c_[np.ones((m, 1)).reshape(-1, 1),
              np.array(dataset[:, 0]).reshape(-1, 1)]
    Y = np.array(dataset[:, 1]).reshape(-1, 1)
    # # theta 设置为列向量 theta=[2,1] !!!这里一定要设置数据类型!!!
    theta = np.array([0, 0], dtype=float, ndmin=2).reshape(-1, 1)
    iterations = 1500
    alpha = 0.01
    cost = computeCost(X, Y, theta)
    j_history = gradientDescent(X, Y, theta, alpha, 1500)
    plt.figure()
    plt.scatter(X[:, 1], Y, c='r', marker='x')
    plt.plot(X[:, 1], np.dot(X, theta))
    plt.xlabel('Profit in $10,000s')
    plt.ylabel('Population of city in 10,1000s')
    plt.title('单边量回归')
    # 可视化损失
    theta0_vals = np.linspace(-10, 10, 100.0)
    theta1_vals = np.linspace(-1, 4, 100.0)
    # 这里必须要加 不然画出来只用中间一条
    theta0_vals, theta1_vals = np.meshgrid(theta0_vals, theta1_vals)
    J_vals = np.zeros((len(theta0_vals), len(theta1_vals)))
    for i in range(len(theta0_vals)):
        for j in range(len(theta1_vals)):
            t = np.array([theta0_vals[i, j], theta1_vals[i, j]]).reshape(-1, 1)
            J_vals[i, j] = computeCost(X, Y, t)
            # print("J_vals[{}, {}]={}".format(i,j,J_vals[i,j]))

    fig1 = plt.figure()
    ax = fig1.gca(projection='3d')
    surf = ax.plot_surface(theta0_vals, theta1_vals, J_vals)
    plt.xlabel('theta0')
    plt.ylabel('theta1')
    plt.title('可视化损失')

    """ 以下为多变量回归 """
    # ===========数据标准化=============

    dataset = load_data('machine_learning_exam/week1/ex1data2.txt')
    m = dataset.shape[0]
    X = np.array(dataset[:, :2])  # x=[m,2]
    Y = np.array(dataset[:, 2]).reshape(-1, 1)  # y=[m,1]
    # 归一化特征值
    X, mu, sigma = featureNormalize(X)
    # x add a cloum
    X = np.c_[np.ones((m, 1)).reshape(-1, 1), X]
    # ===========梯度下降=============

    # 选择学习率
    iterations = 8500
    alpha = 0.01

    # theta 列向量 theta=[3,1]
    theta = np.zeros((3, 1))
    theta, j_history = gradientDescentMulti(X, Y, theta, alpha, iterations)
    # 绘画
    plt.figure()
    plt.plot(range(len(j_history)), j_history, '-b')
    plt.xlabel('Number of iterations')
    plt.ylabel('Cost J')
    plt.title('学习率为:{}'.format(alpha))
    # plt.show()
    print('Theta computed from gradient descent:', theta[:, 0])

    # 估计
    price = np.ones((1, 3))
    price[0, 1:] = (np.array([1650, 3])-mu)/sigma
    price = price@theta
    print('Predicted price of a 1650 sq-ft, 3 br house (using gradient descent):', price)

    """ 以下使用正规方程求解 """
    # ===========数据读取=============

    dataset = load_data('machine_learning_exam/week1/ex1data2.txt')
    m = dataset.shape[0]
    X = np.array(dataset[:, :2])  # x=[m,2]
    Y = np.array(dataset[:, 2]).reshape(-1, 1)  # y=[m,1]
    # x add a cloum
    X = np.c_[np.ones((m, 1)).reshape(-1, 1), X]

    # ===========梯度下降=============
    # 选择学习率
    iterations = 400
    alpha = 0.01

    # theta 列向量 theta=[3,1]
    theta = normalEqn(X, Y)
    # 估计
    print('Theta computed from normal equations:', theta[:, 0])
    price = np.array([1, 1650, 3])@theta
    print('Predicted price of a 1650 sq-ft, 3 br house (using normal equations):', price)
    plt.show()

执行：

➜  Machine_learning /usr/bin/python3 /media/zqh/程序与工程/Python_study/Machine_learning/machine_learning_exam/week1/ex1.py
Theta computed from gradient descent: [ 340412.65957447  110631.05027884   -6649.47427082]
Predicted price of a 1650 sq-ft, 3 br house (using gradient descent): [[ 293081.46433489]]
Theta computed from normal equations: [ 89597.9095428     139.21067402  -8738.01911233]
Predicted price of a 1650 sq-ft, 3 br house (using normal equations): [ 293081.4643349]

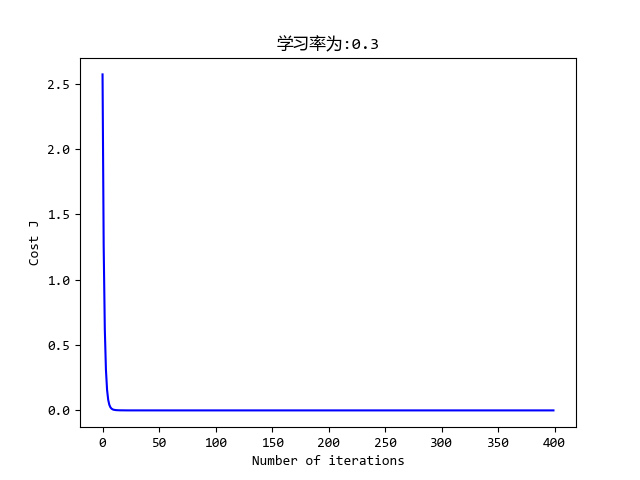
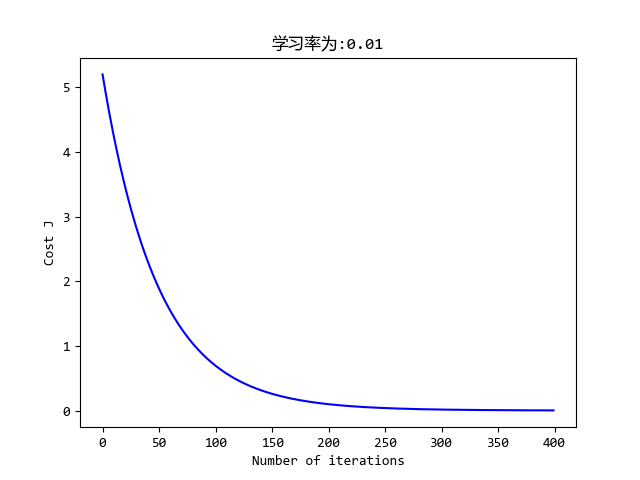
效果

单变量回归