声音信号处理-FFT性质
今天实践FFT的各种性质。
傅里叶属性
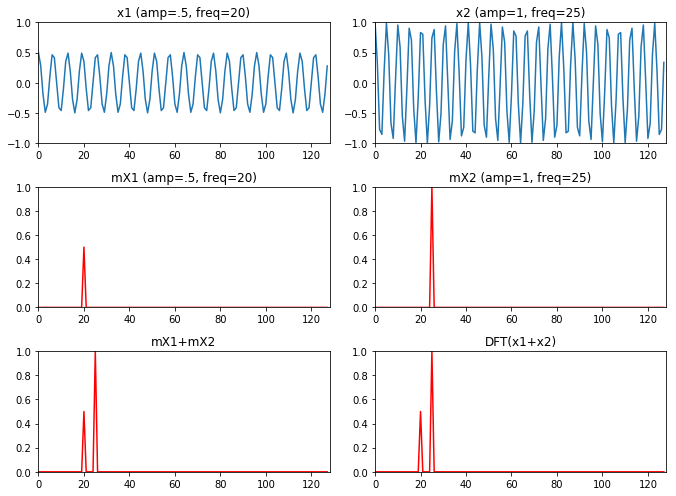
首先从\(x_1\),\(x_2\)两个信号的线性组合开始:
线性:$ ax_1[n]+bx_2[n]aX_1[n]+bX_2[n] $
\[ \begin{align} \because DFT&(ax_1[n]+bx_2[n]) \\ &=\sum^{N-1}_{n=0}(ax_1[n]+bx_2[n])e^{-j2\pi kn/N}\\ &=\sum^{N-1}_{n=0}ax_1[n]e^{-j2\pi kn/N}+\sum^{N-1}_{n=0}bx_2[n]e^{-j2\pi kn/N}\\ &=a\sum^{N-1}_{n=0}x_1[n]e^{-j2\pi kn/N}+b\sum^{N-1}_{n=0}x_2[n]e^{-j2\pi kn/N}\\ &=aX_1[k]+bX_2[k] \end{align} \] 说明两个信号相加,在幅度谱上也是进行相同的相加.
import matplotlib.pyplot as plt |
平移
\[x[n-n_0]\Leftrightarrow e^{-j2\pi kn_0/N}X[k]\] 证明: \[ \begin{align} DFT&(x[n-n_0])\\ &=\sum^{N-1}_{n=0}x[n-n_0]e^{-j2\pi kn/N}\\ &=\sum^{N-1}_{n=0}x[m]e^{-j2\pi k(m+n_0)/N}\ \ \ \ (m=n-n_0)\\ &=\sum^{N-1}_{n=0}x[m]e^{-j2\pi km/N}e^{-j2\pi kn_0/N}\\ &=e^{-j2\pi kn_0/N}\sum^{N-1}_{n=0}x[m]e^{-j2\pi km/N} \\ &=e^{-j2\pi kn_0/N}X[k] \end{align} \] 时域中平移,在DFT之后就相当于乘上特定的sin波形,两个信号的频谱与幅度谱都相同,但是相位谱是不同的.(因为这个是复指数,乘上不会改变幅度)
import matplotlib.pyplot as plt |

对称性
如果一个偶对称的实信号做DFT,那么他的复数谱也是偶对称的,复数谱的虚部是奇对称的. 幅度谱为偶对称,相位谱为奇对称.
import matplotlib.pyplot as plt |

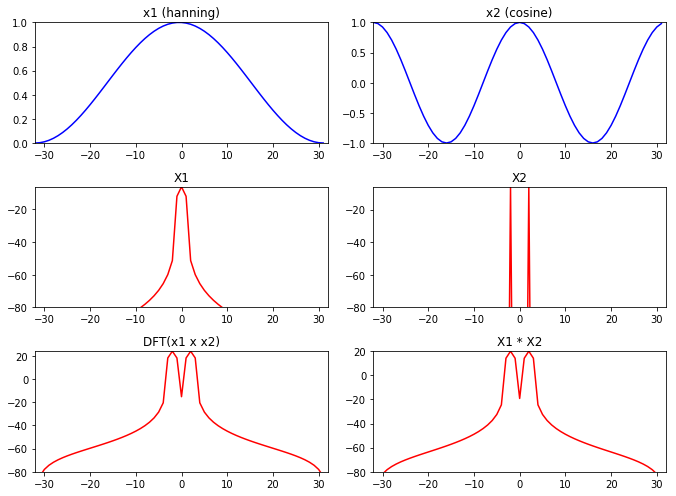
卷积
\[x_1[n] \ast x_2[n]\Leftrightarrow X_1[n] \times X_2[n]\] 证明: \[ \begin{align} DFT&(x_1[n] \ast x_2[n]) \\ &=\sum^{N-1}_{n=0}(x_1[n] \ast x_2[n])e^{-j2\pi kn/N}\\ &=\sum^{N-1}_{n=0}\sum^{N-1}_{m=0}x_1[m]x_2[n-m])e^{-j2\pi kn/N}\\ &=\sum^{N-1}_{m=0}x_1[m]\sum^{N-1}_{n=0}x_2[n-m])e^{-j2\pi kn/N}\\ &=(\sum^{N-1}_{m=0}x_1[m]e^{-j2\pi km/N})X_2[k] \\ &=X_1[k]X_2[k] \end{align} \] 时域的卷积相当于频域的乘法.
import matplotlib.pyplot as plt |
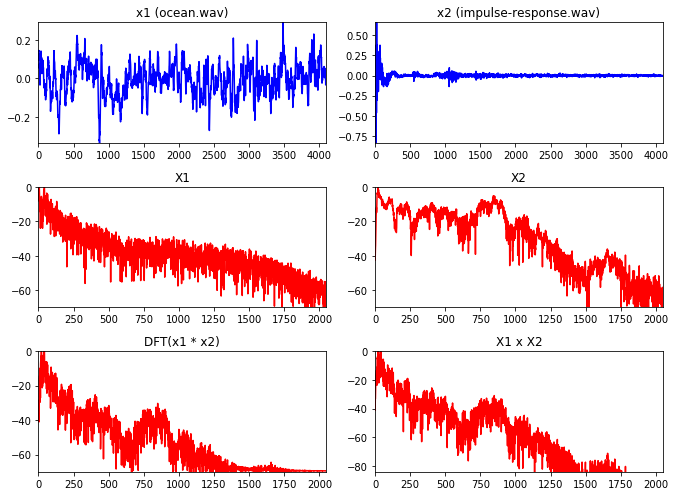
我们可以利用卷积来进行滤波~
import matplotlib.pyplot as plt |
能量卷积
能量被定义为信号的绝对平方根之和,在频域中需要除以N. \[\sum^{N/2-1}_{n=-N/2}|x[n]|^2=\frac{1}{N}\sum^{N/2-1}_{n=-N/2}|X[k]|^2\] 例如: \[\sum^{N/2-1}_{n=-N/2}|x[n]|^2=11.81182\] \[\frac{1}{N}\sum^{N/2-1}_{n=-N/2}|X[k]|^2=11.81182\]
import numpy as np |
11.811824035647202
11.811824035647192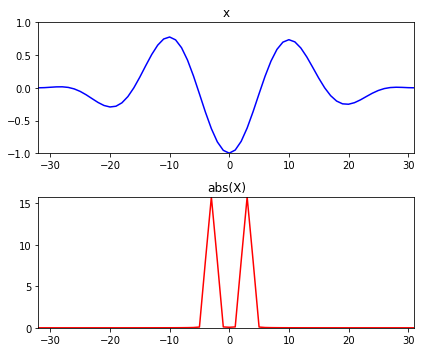
分贝
与能量相关的概念是振幅,所以定义分贝为信号绝对值的20倍log10.
import numpy as np |
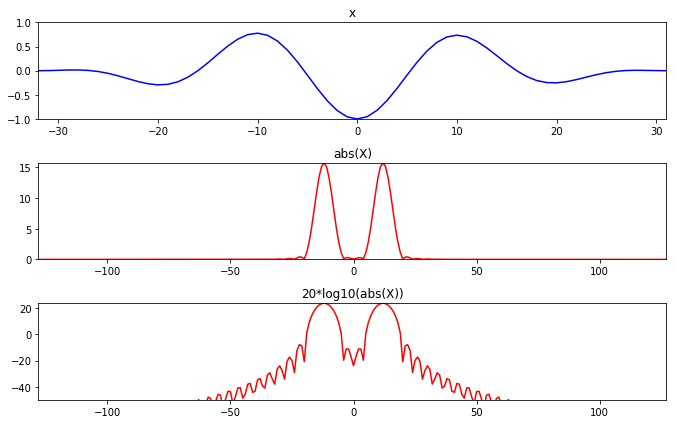
FFT变换
因为DFT计算量较大,FFT则是利用DFT的对称性来达到加速计算的效果.
首先我们看看时间对比:
DFT运算会达到2分钟,成指数级增长.
FFT则快多了,是\(nlogn\)的增长
import numpy as np |
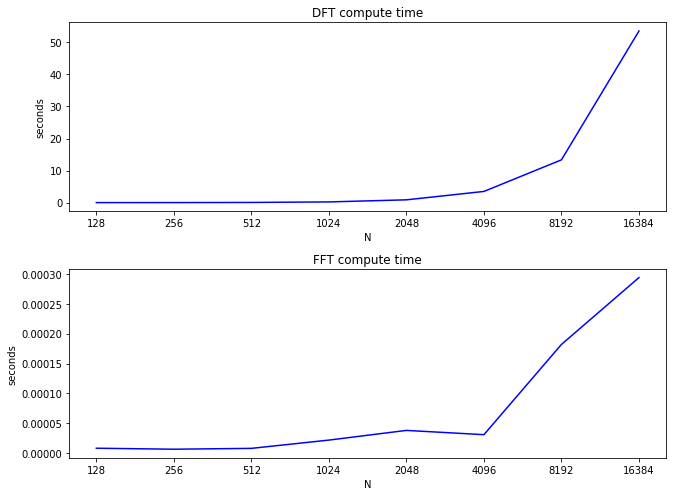
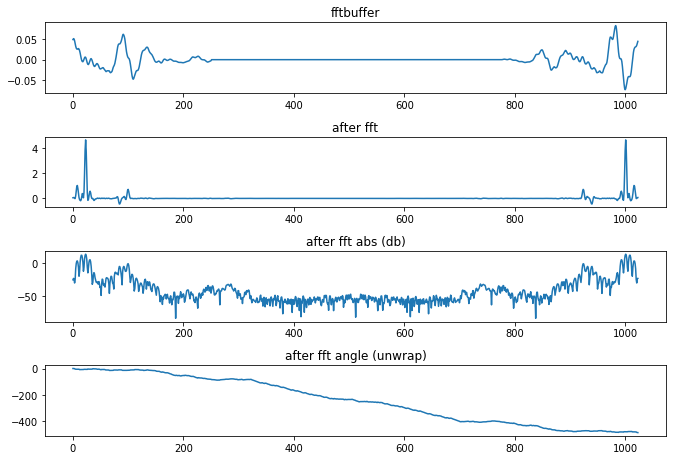
为了使用FFT,我们需要让输入信号具有两个长度的功率.但是我们想要计算任何长度信号的频谱.所以我们需要先做零填充然后使用零相位窗口的方法.看看下面这个例子:
一个401个样本的声音片段.我们需要使用2的幂次,正好下一个2的幂次是512,所以fftbuffer为512,接着给fftbuffer零填充,然后把正样本放到左侧,中间空出,负样本放到右侧.接下来做fft变化
import matplotlib.pyplot as plt |
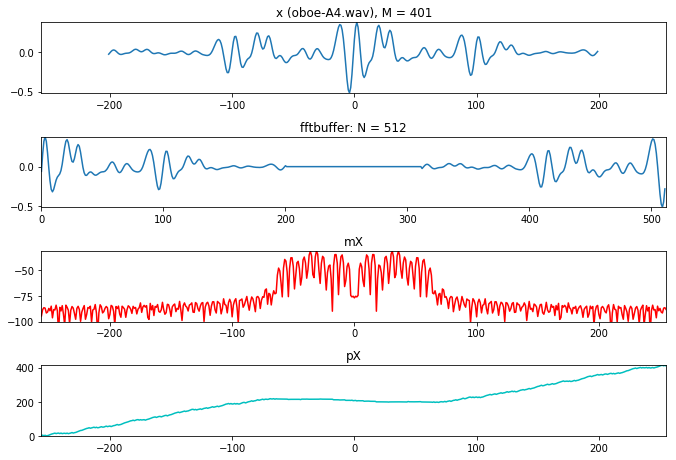
FFT 编程
对三角波进行fft
import numpy as np |

位移三角波再进行fft
x=triang(15) # 生成一个15点三角波 |
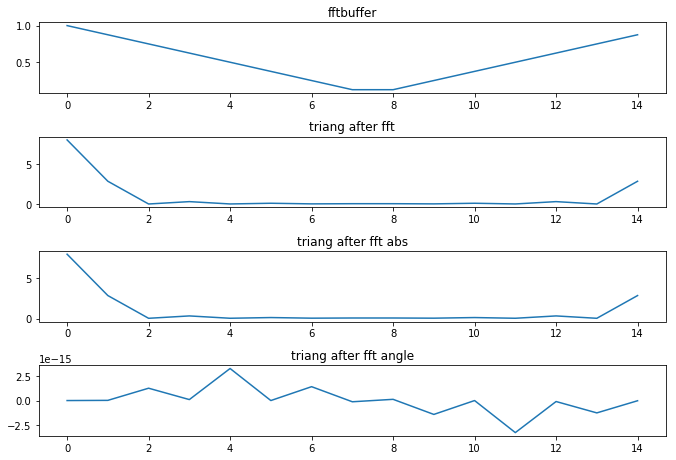
读取真实信号进行fft
取fftbuffer N=511
import utilFunctions as UF |
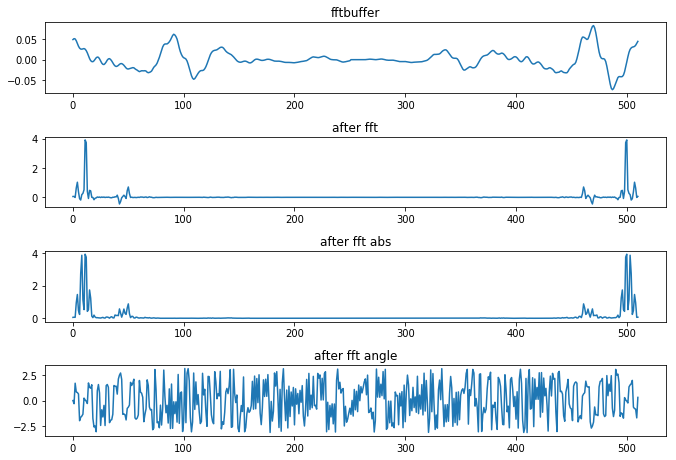
读取真实信号进行fft
取fftbuffer N=1024
import utilFunctions as UF |