短时傅里叶变换
变换方程
\[
\begin{align}
X_l[k]&=\sum^{N/2-1}_{n=-N/2}w[n]x[n+lH]e^{-j2\pi kn/N}\ \ \ \
l=0,1,\ldots, \\
w&= 分析窗口\\
l&= 帧索引\\
H&= 跳跃大小
\end{align}
\]
与DFT几乎没有大的区别,但是有了l,H,是对于一个时间段进行分析.
所以输出不是单个频谱而是一系列频谱,每一个频谱都有相同的长度,但是每一个都相同,因为输入的时间片段是不一样的.
import matplotlib.pyplot as pltimport numpy as npfrom scipy.io.wavfile import read(fs, x) = read('../sounds/oboe-A4.wav' ) M = 256 H = 128 start = int (.8 *fs) plt.figure(1 ) x0 = x[start:start+3 *M]/float (max (x)) plt.plot(x0) plt.axis([0 , 3 *M, min (x0), max (x0)+5.5 ]) offset = 1.5 x1 = np.zeros(3 *M)+offset x1[0 :M] += (x0[0 :M] * np.hamming(M)) plt.plot(x1,'b' ) offset = 2.5 x2 = np.zeros(3 *M)+offset x2[H:M+H] += (x0[H:M+H] * np.hamming(M)) plt.plot(x2,'b' ) offset = 3.5 x2 = np.zeros(3 *M)+offset x2[H*2 :M+H*2 ] += (x0[2 *H:M+H*2 ] * np.hamming(M)) plt.plot(x2,'b' ) offset = 4.5 x2 = np.zeros(3 *M)+offset x2[H*3 :M+H*3 ] += (x0[3 *H:M+H*3 ] * np.hamming(M)) plt.plot(x2,'b' ) offset = 5.5 x2 = np.zeros(3 *M)+offset x2[H*4 :M+H*4 ] += (x0[4 *H:M+H*4 ] * np.hamming(M)) plt.plot(x2,'b' ) plt.tight_layout() plt.show()
可以从上图观察到每一个时间片段的计算情况.
通过使用分析窗口将声音加窗与计算.最后能获得所有声音作为基本片段的总和.
转换一个窗口的正弦波
\[
\begin{aligned}
x[n]&=A_0cos(2 \pi k_0 n/N)=\frac{A_0}{2}e^{j2\pi k_0
n/N}+\frac{A_0}{2}e^{-j2\pi k_0 n/N} \\
X[k]&=\sum^{N/2-1}_{n=-N/2}w[n]x[n]e^{-j2\pi kn/N} \\
&=\sum^{N/2-1}_{n=-N/2}w[n](\frac{A_0}{2}e^{j2\pi k_0
n/N}+\frac{A_0}{2}e^{-j2\pi k_0 n/N})e^{-j2\pi kn/N} \\
&=\sum^{N/2-1}_{n=-N/2}w[n]\frac{A_0}{2}e^{j2\pi k_0 n/N}e^{-j2\pi
kn/N}+\sum^{N/2-1}_{n=-N/2}w[n]\frac{A_0}{2}e^{-j2\pi k_0 n/N}e^{-j2\pi
kn/N}\\
&=\frac{A_0}{2}\sum^{N/2-1}_{n=-N/2}w[n]e^{-j2\pi(k-k_0)n/N}+\frac{A_0}{2}\sum^{N/2-1}_{n=-N/2}w[n]e^{-j2\pi(k+k_0)n/N}
\\
&=\frac{A_0}{2}W[k-k_0]+\frac{A_0}{2}W[k+k_0]
\end{aligned}
\]
首先一个正弦波可以分离成两个复数信号.一个具有正频率一个具有负频率.接下来我们将x带入stft方程中,经过化简得到结果.
结果即为此窗口信号的频谱,频率偏移了输入信号的频率,并乘上了幅度.当然还有另一半(负频率).
import matplotlib.pyplot as pltimport numpy as npfrom scipy.fftpack import fft, ifftN = 256 M = 63 f0 = 1000 fs = 10000 A0 = .8 hN = N//2 hM = (M+1 )//2 fftbuffer = np.zeros(N) X1 = np.zeros(N, dtype='complex' ) X2 = np.zeros(N, dtype='complex' ) x = A0 * np.cos(2 *np.pi*f0/fs*np.arange(-hM+1 ,hM)) plt.figure(1 , figsize=(9.5 , 7 )) w = np.hanning(M) plt.subplot(2 ,3 ,1 ) plt.title('w (hanning window)' ) plt.plot(np.arange(-hM+1 , hM), w, 'b' , lw=1.5 ) plt.axis([-hM+1 , hM, 0 , 1 ]) fftbuffer[:hM] = w[hM-1 :] fftbuffer[N-hM+1 :] = w[:hM-1 ] X = fft(fftbuffer) X1[:hN] = X[hN:] X1[N-hN:] = X[:hN] mX = 20 *np.log10(abs (X1)) plt.subplot(2 ,3 ,2 ) plt.title('mW' ) plt.plot(np.arange(-hN, hN), mX, 'r' , lw=1.5 ) plt.axis([-hN,hN,-40 ,max (mX)]) pX = np.angle(X1) plt.subplot(2 ,3 ,3 ) plt.title('pW' ) plt.plot(np.arange(-hN, hN), np.unwrap(pX), 'c' , lw=1.5 ) plt.axis([-hN,hN,min (np.unwrap(pX)),max (np.unwrap(pX))]) plt.subplot(2 ,3 ,4 ) plt.title('xw (windowed sinewave)' ) xw = x*w plt.plot(np.arange(-hM+1 , hM), xw, 'b' , lw=1.5 ) plt.axis([-hM+1 , hM, -1 , 1 ]) fftbuffer = np.zeros(N) fftbuffer[0 :hM] = xw[hM-1 :] fftbuffer[N-hM+1 :] = xw[:hM-1 ] X = fft(fftbuffer) X2[:hN] = X[hN:] X2[N-hN:] = X[:hN] mX2 = 20 *np.log10(abs (X2)) plt.subplot(2 ,3 ,5 ) plt.title('mXW' ) plt.plot(np.arange(-hN, hN), mX2, 'r' , lw=1.5 ) plt.axis([-hN,hN,-40 ,max (mX)]) pX = np.angle(X2) plt.subplot(2 ,3 ,6 ) plt.title('pXW' ) plt.plot(np.arange(-hN, hN), np.unwrap(pX), 'c' , lw=1.5 ) plt.axis([-hN,hN,min (np.unwrap(pX)),max (np.unwrap(pX))]) plt.tight_layout() plt.show()
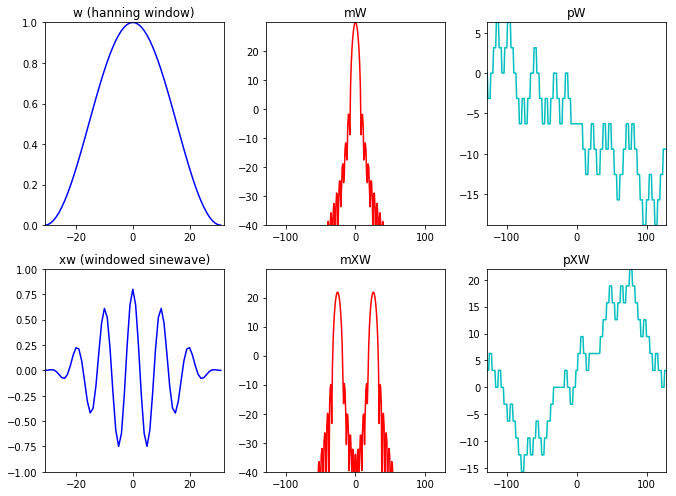
观察上图:
第一幅图是一个汉宁窗,下面则是加窗之后的正弦波.上面左边分别为汉宁窗的幅度谱与相位谱.
当我们对加窗之后的正弦波进行DFT之后,可以看到得到的幅度谱与相位谱与上面相似,只是波峰点移动到了正弦波的频率处.并且由于正负频率特性,波形是对称的.
分析窗口
分析窗口通常一个实函数,并且在原点周围是对称的.
关于窗口,中间的主瓣我们主要关注主瓣宽度,对于旁瓣我们关注与旁瓣的最高水平.
矩形窗函数
\[
\begin{aligned}
w[n]&=\begin{cases}
1,\ \ \ n=-M/2,\ldots,0,\ldots,M/2 \\
0,\ \ \ n=elsewhere
\end{cases}\\
W[k]&=\frac{sin(\pi k)}{sin(\pi k/M)}
\end{aligned}
\]
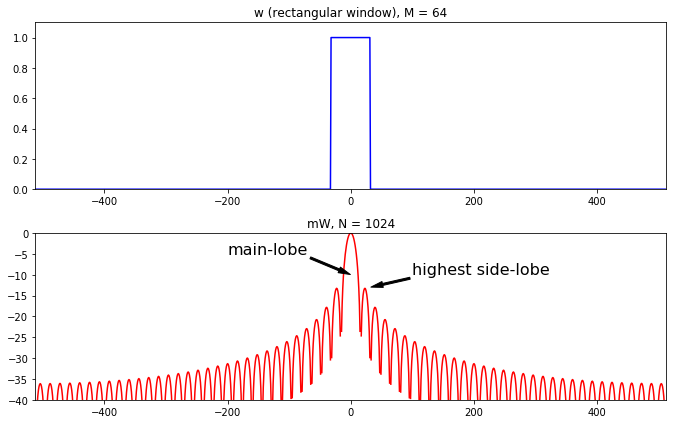
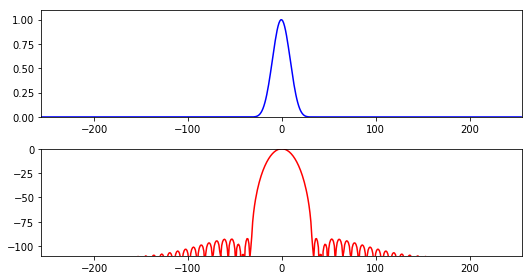
矩形窗是最基础的窗函数,他的时域图形比较简单,但是频域图形相当有趣.
import matplotlib.pyplot as pltimport numpy as npfrom scipy.fftpack import fftM = 64 N = 1024 hN = N//2 hM = M//2 fftbuffer = np.zeros(N) mX1 = np.zeros(N) plt.figure(1 , figsize=(9.5 , 6 )) fftbuffer[hN-hM:hN+hM]=np.ones(M) plt.subplot(2 ,1 ,1 ) plt.plot(np.arange(-hN, hN), fftbuffer, 'b' , lw=1.5 ) plt.axis([-hN, hN, 0 , 1.1 ]) plt.title('w (rectangular window), M = 64' ) X = fft(fftbuffer) mX = 20 *np.log10(abs (X)) mX1[:hN] = mX[hN:] mX1[N-hN:] = mX[:hN] plt.subplot(2 ,1 ,2 ) plt.plot(np.arange(-hN, hN), mX1-max (mX), 'r' , lw=1.5 ) plt.axis([-hN,hN,-40 ,0 ]) plt.title('mW, N = 1024' ) plt.annotate('main-lobe' , xy=(0 ,-10 ), xytext=(-200 , -5 ), fontsize=16 , arrowprops=(dict (facecolor='black' , width=2 , headwidth=6 , shrink=0.01 ))) plt.annotate('highest side-lobe' , xy=(32 ,-13 ), xytext=(100 , -10 ), fontsize=16 , arrowprops=(dict (facecolor='black' , width=2 , headwidth=6 , shrink=0.01 ))) plt.tight_layout() plt.show() print ("主瓣宽度:2bins\n旁瓣最大值:-13.3dB" )
主瓣宽度:2bins
旁瓣最大值:-13.3dB汉明窗
最常用的窗口函数,是一个升余弦函数.
\[
\begin{aligned}
w[n]&=0.5+0.5cos(2\pi n/M),\ \ \ \ n=-M/2,\ldots,0,\ldots,M/2\\
W[k]&=0.5D[k]+0.25(D[k-1]+D[k+1])\ \ \ \ where D[k]=\frac{sin(\pi
k)}{sin(\pi k/M)}
\end{aligned}
\]
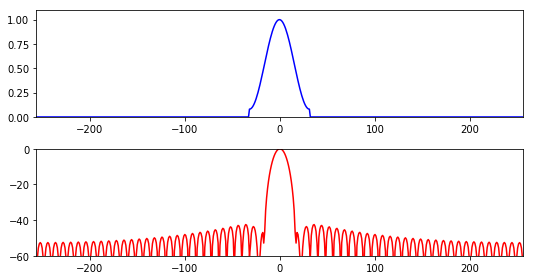
他的主瓣宽度更宽,旁瓣宽度更低.
import matplotlib.pyplot as pltimport numpy as npfrom scipy.fftpack import fftM = 64 N = 512 hN = N//2 hM = M//2 fftbuffer = np.zeros(N) mX1 = np.zeros(N) plt.figure(1 , figsize=(7.5 , 4 )) fftbuffer[hN-hM:hN+hM]=np.hamming(M) plt.subplot(2 ,1 ,1 ) plt.plot(np.arange(-hN, hN), fftbuffer, 'b' , lw=1.5 ) plt.axis([-hN, hN, 0 , 1.1 ]) X = fft(fftbuffer) mX = 20 *np.log10(abs (X)) mX1[:hN] = mX[hN:] mX1[N-hN:] = mX[:hN] plt.subplot(2 ,1 ,2 ) plt.plot(np.arange(-hN, hN), mX1-max (mX), 'r' , lw=1.5 ) plt.axis([-hN,hN,-60 ,0 ]) plt.tight_layout() plt.show() print ("主瓣宽度:4 bins\n旁瓣最高:-42.7dB" )
主瓣宽度:4 bins
旁瓣最高:-42.7dB布莱克曼窗
布莱克曼窗口是两个正弦曲线的总和.
\[
\begin{aligned}
w[n]=0.42-0.5cos(2\pi n/M)+0.08cos(4\pi n/M)
\end{aligned}
\]
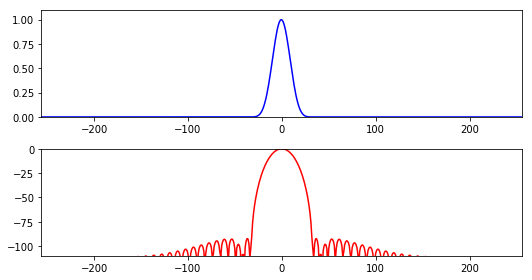
他比汉明窗两侧少了一些突变.所以在旁瓣方面有着显著改善.
import matplotlib.pyplot as pltimport numpy as npfrom scipy.fftpack import fftfrom scipy import signalM = 64 N = 512 hN = N//2 hM = M//2 fftbuffer = np.zeros(N) mX1 = np.zeros(N) plt.figure(1 , figsize=(7.5 , 4 )) fftbuffer[hN-hM:hN+hM]=signal.blackmanharris(M) plt.subplot(2 ,1 ,1 ) plt.plot(np.arange(-hN, hN), fftbuffer, 'b' , lw=1.5 ) plt.axis([-hN, hN, 0 , 1.1 ]) X = fft(fftbuffer) mX = 20 *np.log10(abs (X)) mX1[:hN] = mX[hN:] mX1[N-hN:] = mX[:hN] plt.subplot(2 ,1 ,2 ) plt.plot(np.arange(-hN, hN), mX1-max (mX), 'r' , lw=1.5 ) plt.axis([-hN,hN,-110 ,0 ]) plt.tight_layout() plt.show() print ("主瓣宽度:6 bins\n旁瓣最大值:-58dB" )
主瓣宽度:6 bins
旁瓣最大值:-58dB布莱克曼哈里斯窗
这是一个特殊的窗口.
\[
\begin{aligned}
w(n)=\frac{1}{M}\sum^3_{l=0}\alpha_lcos(2nl\pi /M ),\ \ \ \
n=-M/2,\ldots,0,\ldots,M/2\\
where \alpha_0=0.35875\ \ \alpha_1=0.48829\ \ \alpha_0=0.14128\ \
\alpha_0=0.01168\ \
\end{aligned}
\]
可以说他基本没有旁瓣,他的旁瓣电平低于-92dB。以信噪比的方式去考虑,这是一个非常重要的数字,92dB基本上低于16的底噪。
import matplotlib.pyplot as pltimport numpy as npfrom scipy.fftpack import fftfrom scipy import signalM = 64 N = 512 hN = N//2 hM = M//2 fftbuffer = np.zeros(N) mX1 = np.zeros(N) plt.figure(1 , figsize=(7.5 , 4 )) fftbuffer[hN-hM:hN+hM]=signal.blackmanharris(M) plt.subplot(2 ,1 ,1 ) plt.plot(np.arange(-hN, hN), fftbuffer, 'b' , lw=1.5 ) plt.axis([-hN, hN, 0 , 1.1 ]) X = fft(fftbuffer) mX = 20 *np.log10(abs (X)) mX1[:hN] = mX[hN:] mX1[N-hN:] = mX[:hN] plt.subplot(2 ,1 ,2 ) plt.plot(np.arange(-hN, hN), mX1-max (mX), 'r' , lw=1.5 ) plt.axis([-hN,hN,-110 ,0 ]) plt.tight_layout() plt.show() print ("主瓣宽度:8 bins\n旁瓣最大值:-92dB" )
主瓣宽度:8 bins
旁瓣最大值:-92dB结果比较
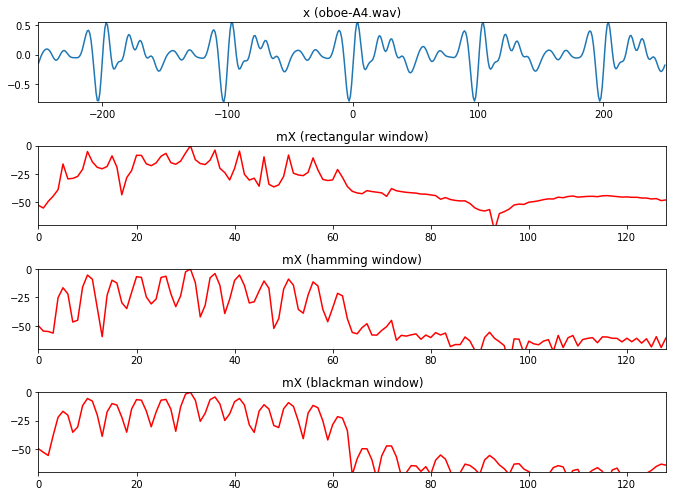
现在比较几个窗口的处理的不同输出结果:
import matplotlib.pyplot as pltimport numpy as npimport time, os, syssys.path.append('../software/models/' ) import dftModel as DFimport utilFunctions as UFfrom scipy.fftpack import fft, ifftimport math(fs, x) = UF.wavread('../sounds/oboe-A4.wav' ) N = 512 pin = 5000 w = np.ones(501 ) hM1 = int (math.floor((w.size+1 )/2 )) hM2 = int (math.floor(w.size/2 )) x1 = x[pin-hM1:pin+hM2] plt.figure(1 , figsize=(9.5 , 7 )) plt.subplot(4 ,1 ,1 ) plt.plot(np.arange(-hM1, hM2), x1, lw=1.5 ) plt.axis([-hM1, hM2, min (x1), max (x1)]) plt.title('x (oboe-A4.wav)' ) mX, pX = DF.dftAnal(x1, w, N) mX = mX - max (mX) plt.subplot(4 ,1 ,2 ) plt.plot(np.arange(mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,N/4 ,-70 ,0 ]) plt.title ('mX (rectangular window)' ) w = np.hamming(501 ) mX, pX = DF.dftAnal(x1, w, N) mX = mX - max (mX) plt.subplot(4 ,1 ,3 ) plt.plot(np.arange(mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,N/4 ,-70 ,0 ]) plt.title ('mX (hamming window)' ) w = np.blackman(501 ) mX, pX = DF.dftAnal(x1, w, N) mX = mX - max (mX) plt.subplot(4 ,1 ,4 ) plt.plot(np.arange(mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,N/4 ,-70 ,0 ]) plt.title ('mX (blackman window)' ) plt.tight_layout() plt.show()
窗口尺寸
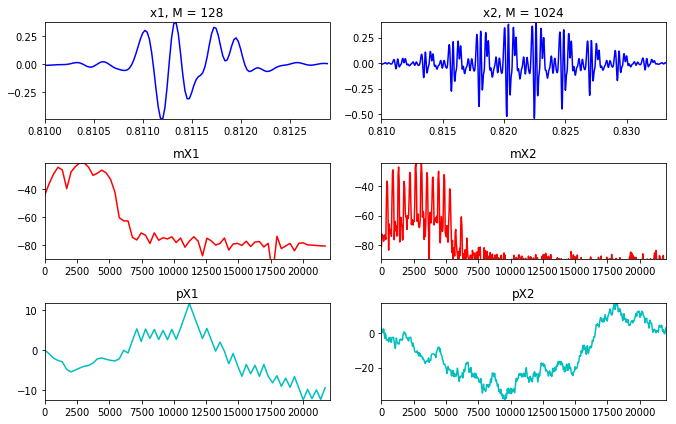
窗口的尺寸当然可以变化,但是尺寸的变化影响着什么? 看下面这个例子:
小窗口我们可以看到谐波很少,信息很少,样本很少.
大窗口样本很多,可以看到更多的声音细节,但是噪音也更加多.
所以这将是一个重要的选择.
(fs, x) = UF.wavread('../sounds/oboe-A4.wav' ) N = 128 start = int (.81 *fs) x1 = x[start:start+N] plt.figure(1 , figsize=(9.5 , 6 )) plt.subplot(321 ) plt.plot(np.arange(start, (start+N), 1.0 )/fs, x1*np.hamming(N), 'b' , lw=1.5 ) plt.axis([start/fs, (start+N)/fs, min (x1*np.hamming(N)), max (x1*np.hamming(N))]) plt.title('x1, M = 128' ) mX, pX = DF.dftAnal(x1, np.hamming(N), N) plt.subplot(323 ) plt.plot((fs/2.0 )*np.arange(mX.size)/float (mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,fs/2.0 ,-90 ,max (mX)]) plt.title('mX1' ) plt.subplot(325 ) plt.plot((fs/2.0 )*np.arange(mX.size)/float (mX.size), pX, 'c' , lw=1.5 ) plt.axis([0 ,fs/2.0 ,min (pX),max (pX)]) plt.title('pX1' ) N = 1024 start = int (.81 *fs) x2 = x[start:start+N] mX, pX = DF.dftAnal(x2, np.hamming(N), N) plt.subplot(322 ) plt.plot(np.arange(start, (start+N), 1.0 )/fs, x2*np.hamming(N), 'b' , lw=1.5 ) plt.axis([start/fs, (start+N)/fs, min (x2), max (x2)]) plt.title('x2, M = 1024' ) plt.subplot(324 ) plt.plot((fs/2.0 )*np.arange(mX.size)/float (mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,fs/2.0 ,-90 ,max (mX)]) plt.title('mX2' ) plt.subplot(326 ) plt.plot((fs/2.0 )*np.arange(mX.size)/float (mX.size), pX, 'c' , lw=1.5 ) plt.axis([0 ,fs/2.0 ,min (pX),max (pX)]) plt.title('pX2' ) plt.tight_layout() plt.show()
奇偶窗口
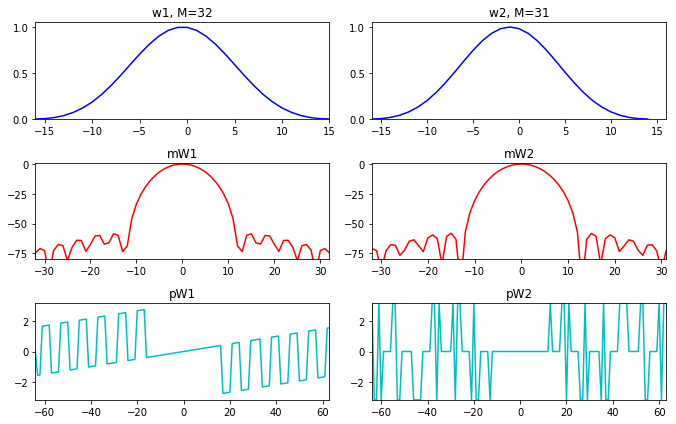
另外的一个问题是,即使一个微小的差异(窗口的奇偶不同),对于相位谱影响巨大.
当我们做fft的时候,最好使用奇数窗口,这样我们的相位谱可以正好对称.
import matplotlib.pyplot as pltimport numpy as npfrom scipy.fftpack import fft, fftshiftfrom scipy import signalM = 32 N = 128 hN = N//2 hM = M//2 fftbuffer = np.zeros(N) w = signal.blackman(M) plt.figure(1 , figsize=(9.5 , 6 )) plt.subplot(3 ,2 ,1 ) plt.plot(np.arange(-hM, hM), w, 'b' , lw=1.5 ) plt.axis([-hM, hM-1 , 0 , 1.05 ]) plt.title('w1, M=32' ) fftbuffer = np.zeros(N) fftbuffer[:hM] = w[hM:] fftbuffer[N-hM:] = w[:hM] X = fft(fftbuffer) mX = 20 *np.log10(abs (fftshift(X))) plt.subplot(3 ,2 ,3 ) plt.plot(np.arange(-hN, hN), mX-max (mX), 'r' , lw=1.5 ) plt.axis([-hN//2 ,hN//2 ,-80 ,1 ]) plt.title('mW1' ) pX = np.angle(fftshift(X)) plt.subplot(3 ,2 ,5 ) plt.plot(np.arange(-hN, hN), pX, 'c' , lw=1.5 ) plt.axis([-hN,hN-1 ,-np.pi,np.pi]) plt.title('pW1' ) M = 31 N = 128 hN = N//2 hM = (M+1 )//2 fftbuffer = np.zeros(N) w = signal.blackman(M) plt.subplot(3 ,2 ,2 ) plt.plot(np.arange(-hM, hM-1 ), w, 'b' , lw=1.5 ) plt.axis([-hM, hM, 0 , 1.05 ]) plt.title('w2, M=31' ) fftbuffer = np.zeros(N) fftbuffer[:hM] = w[hM-1 :] fftbuffer[N-hM+1 :] = w[:hM-1 ] X = fft(fftbuffer) mX = 20 *np.log10(abs (fftshift(X))) plt.subplot(3 ,2 ,4 ) plt.plot(np.arange(-hN, hN), mX-max (mX), 'r' , lw=1.5 ) plt.axis([-hN/2 ,hN/2 -1 ,-80 ,1 ]) plt.title('mW2' ) pX = np.angle(fftshift(X)) plt.subplot(3 ,2 ,6 ) plt.plot(np.arange(-hN, hN), pX, 'c' , lw=1.5 ) plt.axis([-hN,hN-1 ,-np.pi,np.pi]) plt.title('pW2' ) plt.tight_layout() plt.show()
FFT尺寸
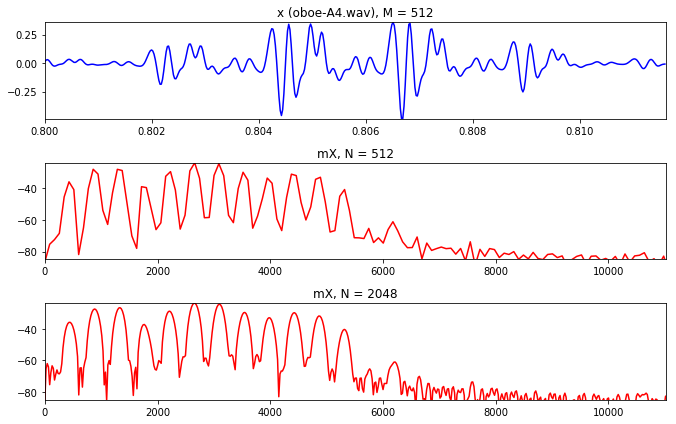
从给定的512窗口大小开始,我们选择不同的FFT尺寸,第一幅图我们可以得到一个不错的图.当尺寸更大的时候我们可以得到更加光滑的图片.
import mathimport matplotlib.pyplot as pltimport numpy as npimport time, os, sys(fs, x) = UF.wavread('../sounds/oboe-A4.wav' ) M = 512 N = 512 start = int (.8 *fs) x1 = x[start:start+M] xw = x1 * np.hamming(M) plt.figure(1 , figsize=(9.5 , 6 )) plt.subplot(311 ) plt.plot(np.arange(start, (start+M), 1.0 )/fs, xw, 'b' , lw=1.5 ) plt.axis([start/fs, (start+M)/fs, min (xw), max (xw)]) plt.title('x (oboe-A4.wav), M = 512' ) mX, pX = DF.dftAnal(x1, np.hamming(N), N) plt.subplot(312 ) plt.plot((fs/2.0 )*np.arange(mX.size)/float (mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,fs/4.0 ,-85 ,max (mX)]) plt.title('mX, N = 512' ) M = 512 N = 2048 start = int (.8 *fs) x1 = x[start:start+M] xw = x1 * np.hamming(M) mX, pX = DF.dftAnal(x1, np.hamming(M), N) plt.subplot(313 ) plt.plot((fs/2.0 )*np.arange(mX.size)/float (mX.size), mX, 'r' , lw=1.5 ) plt.axis([0 ,fs/4.0 ,-85 ,max (mX)]) plt.title('mX, N = 2048' ) plt.tight_layout() plt.show()
跳跃
这是窗函数的步进长度,称为跳跃.
下面展示两个不同的跳跃大小所带来的变化.
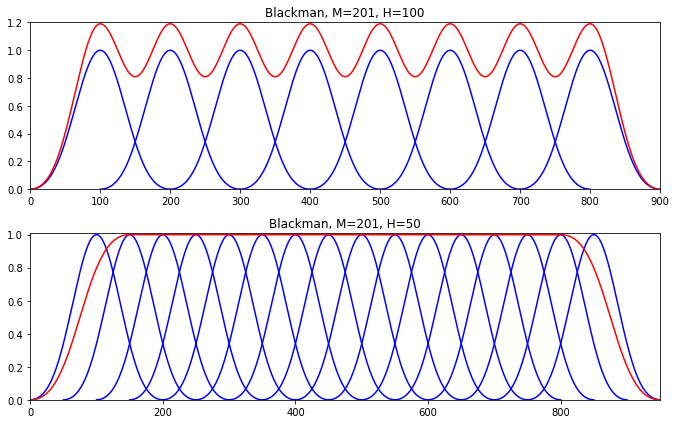
第一个例子,窗口大小为201,跳跃大小为100,大约窗大小的一半.红色线条是窗口的总和,可以看到这个总和不是很好,在震荡.
第二个例子,跳跃大小为窗口大小的四分之一.现在所得到的总和就是我们所需要的.
plt.figure(1 , figsize=(9.5 , 6 )) N= 1000 M = 201 w = signal.blackman(M) w1 = w/sum (w) y = np.zeros(N) H = 100 pin = 0 pend = N - M plt.subplot(211 ) while pin<pend: y [pin:pin+M] += w1*H plt.plot(np.arange(pin, pin+M), w, 'b' , lw=1.5 ) pin += H plt.plot(np.arange(0 , N), y, 'r' , lw=1.5 ) plt.axis([0 , N-H, 0 , max (y)+.01 ]) plt.title('Blackman, M=201, H=100' ) y = np.zeros(N) H = 50 pin = 0 pend = N - M plt.subplot(212 ) while pin<pend: y [pin:pin+M] += w1*H plt.plot(np.arange(pin, pin+M), w, 'b' , lw=1.5 ) pin += H plt.plot(np.arange(0 , N), y, 'r' , lw=1.5 ) plt.axis([0 , N-H, 0 , max (y)+.01 ]) plt.title('Blackman, M=201, H=50' ) plt.tight_layout() plt.show()
分析真实信号
终于我们掌握了基本原理,可以来分析一下真实的信号:
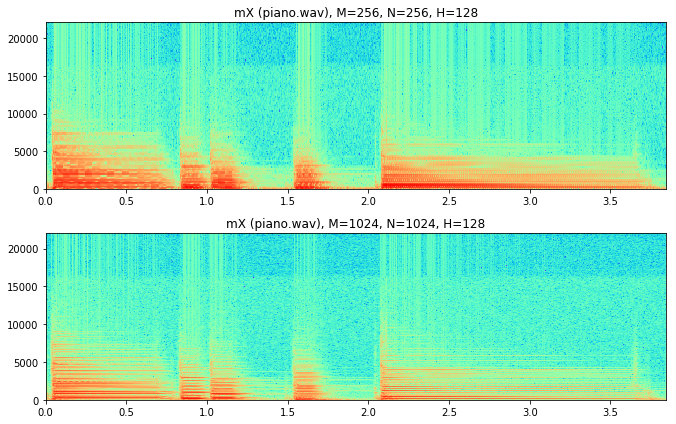
在第一幅图上我们看到的是幅度谱.经过STFT的分析,得到是一个DFT序列.纵轴是频率,横轴是时间,颜色强度是对应的幅值.实际上这就是常说的语谱图.
这里我们可以清楚的看到钢琴的四次敲击,以及横轴对钢琴的谐波反应.对于窗口的大小,如果窗口小,可以得到一个好的时间分辨率,大的窗口会得到较好的频率分辨率.
import numpy as npimport time, os, sysimport stft as STFTimport utilFunctions as UFimport matplotlib.pyplot as pltfrom scipy.signal import hammingfrom scipy.fftpack import fftimport math(fs, x) = UF.wavread('../sounds/piano.wav' ) plt.figure(1 , figsize=(9.5 , 6 )) w = np.hamming(256 ) N = 256 H = 128 mX1, pX1 = STFT.stftAnal(x, w, N, H) plt.subplot(211 ) numFrames = int (mX1[:,0 ].size) frmTime = H*np.arange(numFrames)/float (fs) binFreq = np.arange(mX1[0 ,:].size)*float (fs)/N plt.pcolormesh(frmTime, binFreq, np.transpose(mX1),cmap=plt.get_cmap('rainbow' )) plt.title('mX (piano.wav), M=256, N=256, H=128' ) plt.autoscale(tight=True ) w = np.hamming(1024 ) N = 1024 H = 128 mX2, pX2 = STFT.stftAnal(x, w, N, H) plt.subplot(212 ) numFrames = int (mX2[:,0 ].size) frmTime = H*np.arange(numFrames)/float (fs) binFreq = np.arange(mX2[0 ,:].size)*float (fs)/N plt.pcolormesh(frmTime, binFreq, np.transpose(mX2),cmap=plt.get_cmap('rainbow' )) plt.title('mX (piano.wav), M=1024, N=1024, H=128' ) plt.autoscale(tight=True ) plt.tight_layout() plt.show()
分析STFT的幅度谱和相位谱
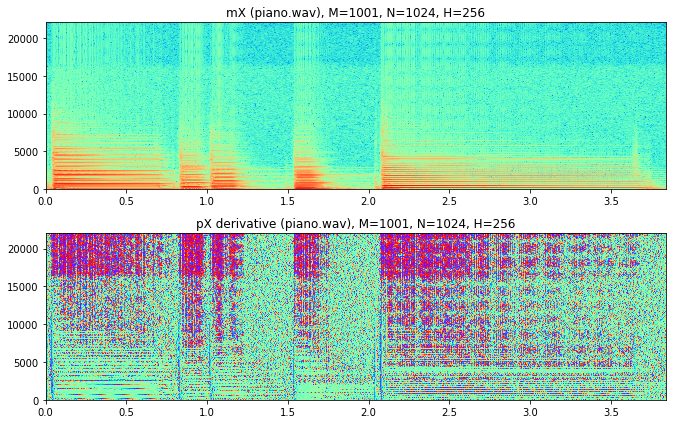
我们也可以可视化幅度谱和相位谱
import stft as STFTimport utilFunctions as UFimport matplotlib.pyplot as pltfrom scipy.signal import hammingfrom scipy.fftpack import fftimport math(fs, x) = UF.wavread('../sounds/piano.wav' ) w = np.hamming(1001 ) N = 1024 H = 256 mX, pX = STFT.stftAnal(x, w, N, H) plt.figure(1 , figsize=(9.5 , 6 )) plt.subplot(211 ) numFrames = int (mX[:,0 ].size) frmTime = H*np.arange(numFrames)/float (fs) binFreq = np.arange(N/2 +1 )*float (fs)/N plt.pcolormesh(frmTime, binFreq, np.transpose(mX),cmap=plt.get_cmap('rainbow' )) plt.title('mX (piano.wav), M=1001, N=1024, H=256' ) plt.autoscale(tight=True ) plt.subplot(212 ) numFrames = int (pX[:,0 ].size) frmTime = H*np.arange(numFrames)/float (fs) binFreq = np.arange(N/2 +1 )*float (fs)/N plt.pcolormesh(frmTime, binFreq, np.diff(np.transpose(pX),axis=0 ),cmap=plt.get_cmap('rainbow' )) plt.title('pX derivative (piano.wav), M=1001, N=1024, H=256' ) plt.autoscale(tight=True ) plt.tight_layout() plt.show()
逆STFT
与IDFT相同,我们当然可以计算ISTFT.因为STFT计算出每个帧单独的频谱,所以我们采用每个帧的逆变换,最终累加.
\[
\begin{aligned}
y[n]=\sum^{L-1}_{l=0}Shift_{lH,n}[\frac{1}{N}\sum^{N/2-1}_{k=-N/2}X_l[k]e^{j2\pi
kn/N}]
\end{aligned}
\] 每次的输出帧: \[
\begin{aligned}
yw_l[n]=x(n+lH)w[n]
\end{aligned}
\] 以及输出音频信号: \[
\begin{aligned}
y[n]=\sum^{L-1}_{l=0}yw_l[n]=x[n]\sum^{L-1}_{l=0}w[n-lH]
\end{aligned}
\]
编程指南
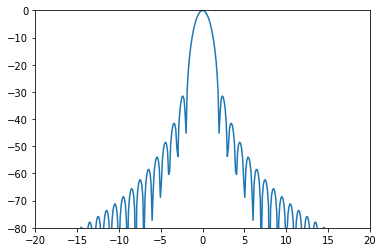
import numpy as npfrom scipy.signal import get_windowfrom scipy.fftpack import fftimport mathimport matplotlib.pyplot as pltM=63 window=get_window('hanning' ,M) hM1=int (math.floor((M+1 )/2 )) hM2=int (math.floor(M/2 )) N=512 hN=int (N/2 ) fftbuffer=np.zeros(N) fftbuffer[:hM1]=window[hM2:] fftbuffer[N-hM2:]=window[:hM2] X=fft(fftbuffer) absX=abs (X) absX[absX<np.finfo(float ).eps]=np.finfo(float ).eps mX=20 *np.log10(absX) pX=np.angle(X) mX1=np.zeros(N) pX1=np.zeros(N) mX1[:hN]=mX[hN:] mX1[N-hN:]=mX[:hN] pX1[:hN]=pX[hN:] pX1[N-hN:]=pX[:hN] plt.plot(np.arange(-hN,hN)/float (N)*M,mX1-max (mX1)) plt.axis([-20 ,20 ,-80 ,0 ]) plt.show()
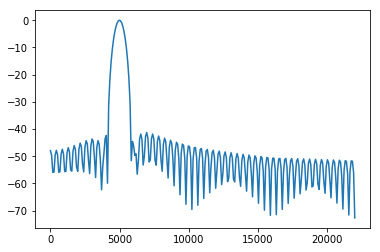
import numpy as npfrom scipy.signal import get_windowfrom scipy.fftpack import fftimport mathsys.path.append('../software/models/' ) import matplotlib.pyplot as pltimport dftModel as DFTfs=44100 f=5000.0 M=101 x=np.cos(2 *np.pi*f*np.arange(M)/fs) N=512 w=get_window('hamming' ,M) mX,pX=DFT.dftAnal(x,w,N) plt.plot(np.arange(0 ,fs//2 ,fs//N),mX-max (mX)) plt.show()
STFT
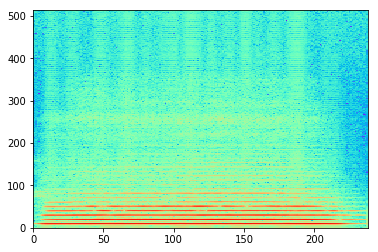
import numpy as npimport matplotlib.pyplot as pltimport os,sysfrom scipy.signal import get_windowsys.path.append('../software/models/' ) import utilFunctions as UFimport stft as STFTinputfile='../sounds/flute-A4.wav' window='hamming' M=801 N=1024 H=400 fs,x=UF.wavread(inputfile) w=get_window(window,M) mX,pX=STFT.stftAnal(x,w,N,H)
plt.pcolor(mX.T,cmap=plt.get_cmap('rainbow' ))