变分自编码器(VAE)学习

我看了VAE之后忽然对神经网络的非监督学习以及概率模型很感兴趣,但是无奈概率模型真的好难懂啊. 今天尝试一边描述VAE一边真正的理解他. 参考总结自:https://spaces.ac.cn/archives/5253

介绍

变分自编码器是传统编码器的一个变体,从深度学习的角度来说就是改变了loss函数使生成器可以 生成与原样本不相同但又属于相同分布的样本.

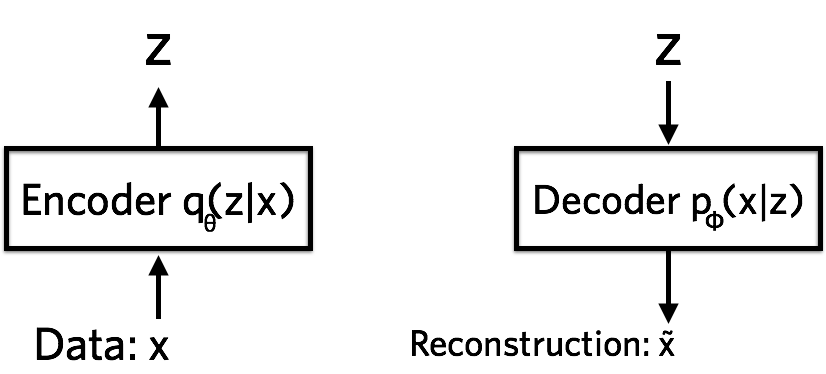
术语表:

• 编码器:

  在概率模型中,编码器称为推理网络,他将参数化潜在特征的后验近似$z$,然后将参数输出到分布$q(z|x)$,也可以说$q(z|x)$是$x$的后验分布.

• 解码器:

  解码器是根据$z$重构$x$的,分布为$p(x|z)$.

推导

在传统的编码器中,解码器$p(x|z)$是易于训练的,但是$q(z|x)$是难以学习的.根据贝叶斯定理,我们可以把后验分布转写成另一种形式,但是$p(x)$也并不知道,所以利用联合概率分布近似代替$p(x)$: $$\begin{aligned} q(z|x)=\frac{p(x|z)p(z)}{p(x)}=\frac{p(x|z)p(z)}{\sum_zp(x|z)p(z)} \end{aligned}$$

为了近似求出后验分布,我们还需要一种方法将估计出的分布与真实分布进行比较,所以使用KL分歧来衡量两个概率分布的相似程度.如果相同,则分歧为0,如果大于0,则分布不同. 因此使用如下方式使用KL分歧: 由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可: $$\begin{aligned}&KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)\\ =&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \left(\log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-x^2/2}/\sqrt{2\pi}}\right)dx\\ =&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \log \left\{\frac{1}{\sqrt{\sigma^2}}\exp\left\{\frac{1}{2}\big[x^2-(x-\mu)^2/\sigma^2\big]\right\} \right\}dx\\ =&\frac{1}{2}\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \Big[-\log \sigma^2+x^2-(x-\mu)^2/\sigma^2 \Big] dx \\ =&\frac{1}{2}[-log\sigma^2+\mu^2+\sigma^2-1] \end{aligned}$$

重参数

VAE可以生成新的$X$就是因为他从隐空间取$z$的时候是随机选取的,但是随机选取$z$会导致无法反向求导,所以就使用一个重参数技巧.

从$N(\mu,\sigma^2)$中采样一个$z$,就相当于从$N(0,1)$中采样一个$\epsilon$,然后令$z=\mu+\epsilon*\sigma$.

本质结构

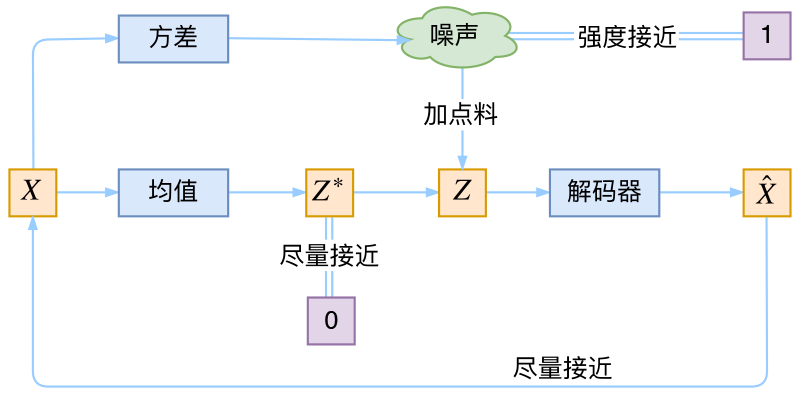
本质上VAE就是训练出一个后验分布$q(Z|X)$,然后生成器从后验分布中随机取元素(相当于加噪声)并解码出对应的$\bar{X}$.代码上实现起来相当简单,但是背后的数学思想是非常难理解的,现在我还是一知半解.