半监督学习:ReMixMatch
第九个算法ReMixMatch: Semi-Supervised Learning with Distribution Alignment and Augmentation Anchoring,这也是谷歌MixMatch的同一作者提出的,是对MixMatch的改进。
算法理论
通过引入两个技术:Distribution Alignment和Augmentation Anchoring改进了MixMatch。
Distribution Alignment
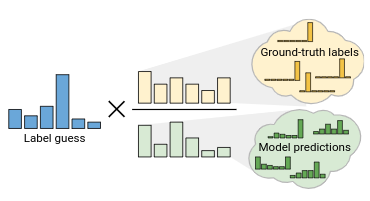
分布对齐的目标是使无标签数据的预测汇总与提供的标签数据分布相匹配。这个概念是25年前的Unsupervised classifiers, mutualinformation and’phantom targets所引入的,但是在ReMixMatch之前还没有人在半监督学习中用过这个方法。
半监督算法的主要目标是利用未标记数据提升模型性能,bridle等人首先提出一种这种直觉形式化的方法,最大化无标签数据的输入与输出间的互信息。将此操作公式化为如下,以下公式推导时,假设了\(p(x),p(y)\)相互独立则有\(p(y) = \int p(x)p(y|x)\ dx\)。:
\[ \begin{align} \mathcal{I}(y ; x) &=\iint p(y, x) \log \frac{p(y, x)}{p(y) p(x)} \mathrm{d} y \mathrm{d} x\\ &=\int p(x) \mathrm{d} x \int p(y | x) \log \frac{p(y | x)}{p(y)} \mathrm{d} y\\ &=\int p(x) \mathrm{d} x \int p(y | x) \log \frac{p(y | x)}{\int p(x) p(y | x) \mathrm{d} x} \mathrm{d} y\\ &=\mathbb{E}_{x}\left[\int p(y | x) \log \frac{p(y | x)}{\mathbb{E}_{x}[p(y | x)]} \mathrm{d} y\right]\\ \text{离散化:}\\ &=\mathbb{E}_{x}\left[\sum_{i=1}^{L} p\left(y_{i} | x\right) \log \frac{p\left(y_{i} | x\right)}{\mathbb{E}_{x}\left[p\left(y_{i} | x\right)\right]}\right]\\ &=\mathbb{E}_{x}\left[\sum_{i=1}^{L} p\left(y_{i} | x\right) \log p\left(y_{i} | x\right)\right]-\mathbb{E}_{x}\left[\sum_{i=1}^{L} p\left(y_{i} | x\right) \log \mathbb{E}_{x}\left[p\left(y_{i} | x\right)\right]\right]\\ &=\mathbb{E}_{x}\left[\sum_{i=1}^{L} p\left(y_{i} | x\right) \log p\left(y_{i} | x\right)\right]-\sum_{i=1}^{L} \mathbb{E}_{x}\left[p\left(y_{i} | x\right)\right] \log \mathbb{E}_{x}\left[p\left(y_{i} | x\right)\right] \end{align}\tag{1} \] \[ \begin{align} &=\mathcal{H}\left(\mathbb{E}_{x}\left[p_{\text {model }}(y | x ; \theta)\right]\right)-\mathbb{E}_{x}\left[\mathcal{H}\left(p_{\text {model }}(y | x ; \theta)\right)\right] \end{align}\tag{2} \]
其中\(\mathcal{H}(\cdot)\)为熵。其中公式2是熟悉的熵最小化目标,它简单的鼓励模型输出具有更低的熵(对当前类别标签置信度更高)。但其中公式1并未广泛使用,其目标是鼓励模型在整个训练集平均预测每个类别的频率相同,bridle等人称之为公平性。
在MixMatch中已经使用了sharpening函数使猜测标签的熵最小化。现在要通过互信息的概念引入公平性这一原则,注意目标\(\mathcal{H}\left(\mathbb{E}_{x}\left[p_{\text
{model }}(y | x ;
\theta)\right]\right)\)本来已经暗示了它应该以相同的频率预测每个标签,但如果数据集中的\(p(y)\)的分布并不是均匀的,那这个目标就不一定有效了。虽然可以按batch最小化这个目标,但是为了不引入更多的超参数,因此为了解决以上问题,引入了另外一种公平性形式Distribution Alignment。其过程如下:
训练过程中维持模型对未标记数据的预测结果的平均值\(\tilde{p}(y)\),给定模型在未标记数据\(u\)上的预测为\(q=P_{\text{model}}(y|u,\theta)\),我们将利用\(\frac{p(y)}{\tilde{p}(y)}\)作为比例缩放\(q\),然后在重新放大到有效的概率分布区间:
\(\tilde{q}=\text{Normalize}(q\times\frac{p(y)}{\tilde{p}(y)})\),其中Normalize为\(\text{Normalize}(x)_i=\frac{x_i}{\sum_j
x_j}\)。 然后我们使用\(\tilde{q}\)作为\(u\)的猜测标签,然后可以再用sharpening或其他的处理方式。实际操作中,将计算过去128个batch中无标签数据预测值的滑动平均作为\(\tilde{p}(y)\),如果我们直接知道\(\tilde{p}(y)\)的某些先验分布,那么应该还可以更好。
改进一致性正则化
论文中说,使用了最新提出AutoAugment数据增强算法来代替原本MixMatch中的数据弱增强看看能不能提高性能,但是发现训练并不能收敛。因此提出了一个解决方法Augmentation Anchoring,它的基本想法是将模型对弱增强的未标记图像的预测结果作为同一图像的强增强的猜测标签。
同时因为AutoAugment是使用强化学习策略来搜索的,需要对有监督模型做多次尝试。在半监督学习中难以做到,为了解决这个问题,提出了一个名为CTAugment的方法,使用控制理论的思想在线适应,而无需任何形式的基于强化学习的训练。
Augmentation Anchoring
我们假设带有AutoAugment的MixMatch不稳定的原因是MixMatch对\(K\)个的预测取了平均值。由于增强效果可能会导致不同的预测,因此其平均值可能不是有意义的目标,取而代之的是,给定一个未标记的输入\(u\),我们首先通过对其应用弱增强来生成一个Anchor。然后使用CTAugment生成\(K\)个\(u\)的增强,然后将(经过distribution alignment和sharpening后的)猜测标签作为\(K\)个增强后的目标。
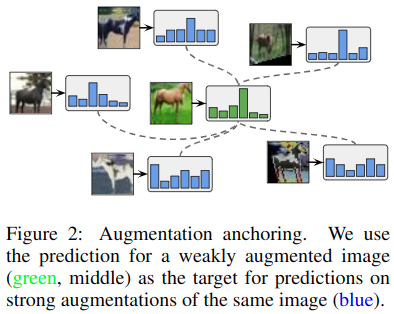
在实验中发现,使用Augmentation Anchoring之后,可以直接使用交叉熵代替原本的mse损失,更易于实现,同时\(K=2\)即可取得不错的效果,当然\(K>8\)效果更好。
Control Theory Augment
像AutoAugment一样,CTAugment均匀的随机采样要实施的变换,但是会在训练过程中动态推断每次变换的幅度大小。由于CTAugment具有不敏感的超参数,因此可以直接包含在半监督模型中。直观的,对于每个建议的参数,CTAugment都知道它将产生被分类正确标签的图像的概率,然后使用这些概率,仅对网络可忍受范围内的误差进行采样。这个过程在FastAutoAugment中被称为density-matching。
首先,CTAugment将每个变化的每个参数范围划分为数个分组,在开始训练时将每个分组的权重设置为1,然后令权重向量\(m\)向某些分组变化,这些权重决定了那些幅度级别是需要实施变化的。在每个训练step中,对于每个图像随机地均匀采样两个变换,用于图像增强。使用改变过的权重参数\(\bar{m}\),其中${m}_i=m_i
m_i>0.8 {m}i =0 \(,否则使用\){m}\(作为权重进行随机分类采样。为了更新权重,首先随机地对每个转换参数均匀的采样一个\)m_i\(,将结果转换应用于带标签样本\)x\(以获得增强版本\){x}\(,然后测量模型的预测与标签的匹配程度为\)-|p{}(y|{x};)-p|\(,每个采样权重的权重更新为\)m_i=m_i+(1-)\(,其中\)$是固定的指数衰减超参数。
综合
综合算法流程如下:

主要是生成两个集合\(\mathcal{X}'\)和\(\mathcal{U}'\),由增强后的带标记的有标签无标签数据mixup生成。\(\mathcal{X}'\)和\(\mathcal{U}'\)的标签与猜测标签根据模型预测输入到标准的交叉熵损失中。还有\(\mathcal{U}_1\)是由无标签数据经过单个强增强组成的,并且他的猜测标签没有应用mixup,\(\mathcal{U}_1\)是用在两个额外的损失项中,它能提供很大的改善。
Pre-mixup unlabeled loss: 将\(\mathcal{U}_1\)的猜测标签和预测输入一个单独的交叉熵损失项。
Rotation loss
:最近的结果表明,将自我监督学习的思想应用于半监督学习可以产生出色的性能(
Self-supervised semi-supervised
learning)。将这个想法通过旋转每个图像\(\text{Rotate}(u,r) \in
\mathcal{U}_1\)来整合,\(r \sim
{0,90,180,270}\),然后要求模型将旋转量预测为四类分类问题。
\[ \begin{align} \begin{aligned} \sum_{x, p \in \mathcal{X}^{\prime}} \mathrm{H}\left(p, p_{\text {model }}(y | x ; \theta)\right)+\lambda_{\mathcal{U}} \sum_{u, q \in \mathcal{U}^{\prime}} \mathrm{H}\left(q, p_{\text {model }}(y | u ; \theta)\right) \\ +\lambda_{\hat{u}_{1}} \sum_{u, q \in \hat{\mathcal{U}}_{1}} \mathrm{H}\left(q, p_{\text {model }}(y | u ; \theta)\right)+\lambda_{r} \sum_{u \in \hat{\mathcal{U}}_{1}} \mathrm{H}\left(r, p_{\text {model }}(r | \text { Rotate }(u, r) ; \theta)\right) \end{aligned} \end{align} \]
根据消融测试结果:
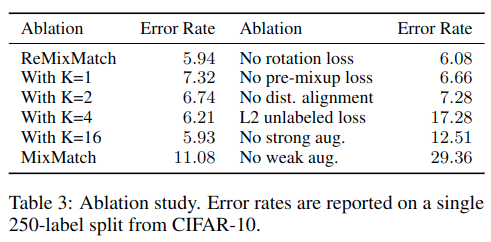
如果没有弱增强和强增强间的augment anchoring错误率就立马上升非常多。其次是将guess label的损失从交叉熵变成l2 loss,不过这里我挺奇怪的,之前其他的算法都是说l2 loss的约束性更大,效果会更好。
代码
def classifier_rot(self, x): |