本文是对旷视所提出的论文：Circle Loss: A Unified Perspective of Pair Similarity Optimization的个人解读。

摘要

Circle Loss对于数据对学习以及分类标签学习提出了一种统一的视角即：最大化类内相似度\(s_p\)，最小化类间相似度\(s_n\)。同时发现对于大多数损失函数，实际是将相似度\(s_p,s_n\)进行嵌入并减小\((s_n-s_p)\)，而传统的损失方式对于每个相似度的惩罚都相等，实际上应该根据不相似的程度进行惩罚。因此提出了Circle Loss，他可以同时对数据对以及分类标签的样本进行学习。

例如triplet loss，softmax loss及其变体具有相似的优化模式。他们都嵌入\(s_n,s_p\)到相似度对，并寻求降低\((s_n-s_p)\)的方法。在\((s_n-s_p)\)中，增加\(s_p\)等效于减少\(s_n\)。这种对称的优化方式容易出现以下两个问题。

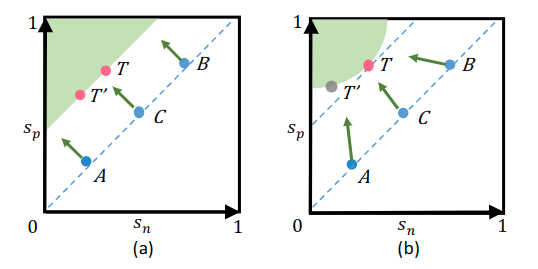
图1，传统方式优化的\(s_n-s_p\)与建议的\(\alpha_n s_n - \alpha_p s_p\)对比。(a)对于A、B、C三点处的梯度均相同，且对于\(T,T'\)的决策面也相同。(b)Circle Loss可以动态调整梯度，使得优化方向更加明确。

缺乏优化的灵活性

对于\(s_n\)和\(s_p\)的惩罚强度被限制为相等，具体在第二节中说明。比如在图1中(a)中的点A，对于决策面已经相当解决了但梯度还是和远离决策面的点相同。

收敛状态不明确

优化\((s_n-s_p)\)通常目标会是一个决策边界\(s_n-s_p=m\)，其中\(m\)为间距。但这个决策面可能会混淆，比如图1中(a)的\(T={s_n:0.2,s_p=0.5}\)与\(T'={s'_n:0.4,s'_p=0.7}\)，虽然他们的间距相同，但\(s'_n\)与\(s_p\)的间距为0.1，因此混淆的决策边界会影响可分离性。

因此针对以上缺点，考虑根据相似度的大小进行惩罚，所以首先推广\((s_n-s_p)\)至\(\alpha_n s_n - \alpha_p s_p\)，其中\(\alpha_n,\alpha_p\)具有独立的权重参数允许\(s_n,s_p\)以不同的速率优化。将\(\alpha_n,\alpha_p\)实现为分别关于\(s_n,s_p\)的线性函数，当相似度与最佳值偏离的越远，加权参数就越大，最终可以得到决策面为\(\alpha_n s_n - \alpha_p s_p=m\)，在\((s_n,s_p)\)空间中为圆形区域，所以称之为Circle Loss。 NOTE: 实际上amsoftmax也是圆形的决策面，可以由Circle Loss退化得到。

统一视角下的损失函数

深度特征学习旨在最大化类内相似度，并最小化类间相似度。例如，在余弦相似度度量下，我们期望\(s_p\rightarrow1\)和\(s_n\rightarrow0\)。为了从统一的视角看待之前众多的损失函数，首先定义如下。给定单个样本\(x\)在特征空间中，有\(K\)个类内相似度分数，\(L\)个类间相似度分数，那么类内相似度分数定义为\(\{s^i_p\}(i=1,2,\ldots,K)\)，类间相似度分数定义为\(\{s^j_n\}(j=1,2,\ldots,L)\)。为了最小化\(s^j_n\)同时最大化\(s^i_p\)，统一的损失函数Unified Loss定义为如下： \[ \begin{aligned} \mathcal{L}_{uni}&=\log\left[1+\sum^K_{i=1}\sum^L_{j=1}\exp(\gamma(s^j_n-s^i_p+m))\right]\\ &=\log\left[1+\sum^L_{j=1}\exp(\gamma(s^j_n+m))\sum^K_{i=1}\exp(\gamma(-s^i_p))\right] \end{aligned}\tag{1} \]

其中\(\gamma,m\)分别为尺度系数与间距系数。现在我们可以尝试修改这个损失函数到之前的损失函数中：

分类标签数据

假设有共有\(N\)类，则嵌入的分类权重向量为\(w_i,i\in\{1,2,\ldots,N\}\)，在am-softmax中最后的全连接层实际上就是分别计算特征\(x\)与权重向量\(w_i\)间的余弦相似度，不太清楚的可以看我之前写的博客。因为分类标签数据所定义的类内标签只有一个，类间标签有\(N-1\)个，然后即可从Unified Loss推导至am-softmax：

\[ \begin{aligned} \mathcal{L}_{uni}&=\log\left[1+\sum^K_{i=1}\sum^L_{j=1}\exp(\gamma(s^j_n-s^i_p+m))\right]\\ &=\log\left[1+\sum^L_{j=1}\exp(\gamma(s^j_n))\sum^K_{i=1}\exp(\gamma(m-s^i_p))\right]\\ \text{Let}\ \ \ \ K&=1,L=N-1\\ \mathcal{L}_{uni}&=\log\left[1+\sum^{N-1}_{j=1}\exp(\gamma(s^j_n))\exp(\gamma(m-s_p))\right]\\ &=-\log\left[\frac{1}{1+\sum^{N-1}_{j=1}\exp(\gamma(s^j_n))\exp(\gamma(m-s_p))}\right]\\ &=-\log\left[\frac{1}{1+\sum^{N-1}_{j=1}\exp(\gamma(s^j_n))\frac{1}{\exp(\gamma(s_p-m))}}\right]\\ &=-\log\left[\frac{\exp(\gamma(s_p-m))}{\exp(\gamma(s_p-m))+\sum^{N-1}_{j=1}\exp(\gamma(s^j_n))}\right]\\ \text{Let}\ \ \ \ s^j_n&=\frac{w^T_jx}{\parallel w_j\parallel \parallel x\parallel }=\cos\theta_j,\ \ s_p=\frac{w^T_{y_i}x}{\parallel w_{y_i}\parallel \parallel x\parallel }=\cos\theta_{y_i}\\ \mathcal{L}_{uni}&=-\log\left[\frac{\exp(\gamma(\cos\theta_{y_i}-m))}{\exp(\gamma(\cos\theta_{y_i}-m))+\sum^{N-1}_{j=1}\exp(\gamma(\cos\theta_j))}\right]\\ \mathcal{L}_{ams} &= - \log \frac{e^{s\cdot(\cos\theta_{y_i} -m)}}{e^{s\cdot (\cos\theta_{y_i} -m)}+\sum^c_{j=1,i\neq t} e^{s\cdot\cos\theta_j }} \end{aligned}\tag{2} \]

当定义相似度指标为余弦距离时，可以看到由Unified Loss推出的倒数第二个公式，和我之前博客中的am-softmax公式是一样的。同时如果将间距系数\(m\)设置为0，比例系数\(\gamma\)设置为1，那么就继续退化到普通的softmax损失了。

配对标签数据

对于配对的标签数据，计算一个batch中\(x\)与其他特征的相似度。特别的，\(s^j_n=\frac{x^T_j x}{\parallel x_j \parallel \parallel x \parallel}\)，其中\(x_j\)为负样本集合\(\mathcal{N}\)中第\(j\)个样本。\(s^i_p= \frac{x^T_i x}{\parallel x_i \parallel \parallel x \parallel}\)，其中\(x_i\)为正样本集合\(\mathcal{P}\)中第\(i\)个样本。相应地\(K=|\mathcal{P}|,L=|\mathcal{N}|\)。则Unified Loss通过难例挖掘退化到triplet loss。

\[ \begin{aligned} \mathcal{L}_{t r i} &=\lim _{\gamma \rightarrow+\infty} \frac{1}{\gamma} \mathcal{L}_{u n i} \\ &=\lim _{\gamma \rightarrow+\infty} \frac{1}{\gamma} \log \left[1+\sum_{i=1}^{K} \sum_{j=1}^{L} \exp \left(\gamma\left(s_{n}^{j}-s_{p}^{i}+m\right)\right)\right] \\ &=\max \left[s_{n}^{j}-s_{p}^{i}\right]_{+} \end{aligned}\tag{3} \]

梯度分析

公式2与公式3展示了由Unified Loss推出的一系列变体，对这些变体进行梯度分析：

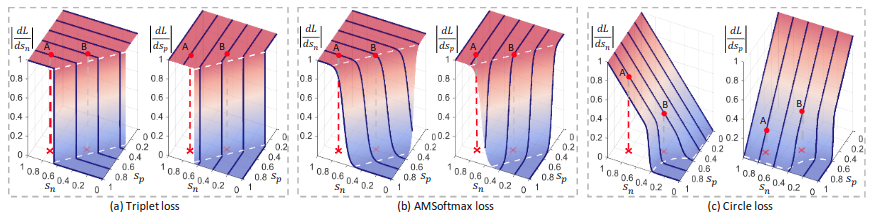
图2：对于a与b，他们的\(s_p\)的梯度相比与\(s_n\)被限制为相等，且梯度会突然减小缺乏连续性。比如点\(A\)的类内相似度已经接近较大值，但梯度依旧较大。同时决策面是平行的，会产生分类混淆。

新的损失函数

自定步数权重

考虑通过允许每个相似性分数按照自己的进度学习，而不依赖于其当前的优化状态，从而提高优化灵活性。首先忽略公式1中的间距参数\(m\)，然后通过以下方法将Unified Loss(公式1)推导至Circle Loss中： \[ \begin{aligned} \mathcal{L}_{\text {circle}} &=\log \left[1+\sum_{i=1}^{K} \sum_{j=1}^{L} \exp \left(\gamma\left(\alpha_{n}^{j} s_{n}^{j}-\alpha_{p}^{i} s_{p}^{i}\right)\right)\right] \\ &=\log \left[1+\sum_{j=1}^{L} \exp \left(\gamma \alpha_{n}^{j} s_{n}^{j}\right) \sum_{i=1}^{K} \exp \left(-\gamma \alpha_{p}^{i} s_{p}^{i}\right)\right] \end{aligned}\tag{4} \]

其中\(\alpha_{n}^{j},\alpha_{p}^{i}\)是非负的权重参数。在训练时\(\alpha_{n}^{j}s^j_n-\alpha_{p}^{i}s^i_p\)的梯度会分布乘上\(\alpha_{n}^{j},\alpha_{p}^{i}\)。假设最优的\(s^i_p\)为\(O_p\)，最优的\(s^j_n\)为\(O_n\)且\((O_n<O_p)\)。当相似度与最优值差距较大时，应该具有较大的权重以便有效更新，权重参数定义如下：

\[ \begin{aligned}\alpha_{p}^{i}=[O_p-s^i_p]_+ \\ \alpha_{n}^{j}=[s^j_n-O_n]_+ \end{aligned}\tag{5} \]

其中\([\cdot]_+\)表示从0截断运算符，保证权重参数非负。通常损失中都带有缩放因子\(\gamma\)，不过Circle Loss的加权项实际代替了缩放因子的作用，不过就算加上缩放因子也没有问题，因为自适应加权项会自适应。

传统基于softmax的损失函数通常把分类问题解释为样本属于某个类别的概率，而概率要求向量的相似度计算要在相同的缩放因子下进行。Circle Loss通过自适应加权放弃了这种观点，使用相似对优化的观点，这样可以更灵活的进行优化。

内类间距与类间间距参数

对于优化\((s_n-s_p)\)，添加间距参数\(m\)可以加权优化性能。因为\(s_n\)和\(-s_p\)具有零点对称性，因此对\(s_n\)添加正间距相当于对\(s_p\)添加负间距。但Circle Loss中\(s_n\)和\(s_p\)不具有零点对称性，因此需要考虑\(s_n\)和\(s_p\)各自的间距： \[ \begin{aligned} \mathcal{L}_{\text {circle}}=\log \left[1+\sum_{j=1}^{L} \exp \left(\gamma \alpha_{n}^{j}\left(s_{n}^{j}-\Delta_{n}\right)\right) \sum_{i=1}^{K} \exp \left(-\gamma \alpha_{p}^{i}\left(s_{p}^{i}-\Delta_{p}\right)\right)\right] \end{aligned}\tag{6} \]

其中\(\Delta_{n},\Delta_{p}\)分别为类间间距参数和类内间距参数。在公式6中，Circle Loss期望\(s_{p}^{i}>\Delta_{p}\)，\(s_{n}^{j}<\Delta_{n}\)。

通过推导决策边界进一步分析\(\Delta_{n}\)与\(\Delta_{p}\)的设置，简单起见，考虑二分类的情况下决策面为\(\alpha_{n}\left(s_{n}-\Delta_{n}\right)-\alpha_{p}\left(s_{p}-\Delta_{p}\right)=0\)。带入公式5与公式6得到决策边界为： \[ \begin{aligned} \left(s_{n}-\frac{O_{n}+\Delta_{n}}{2}\right)^{2}+\left(s_{p}-\frac{O_{p}+\Delta_{p}}{2}\right)^{2}=C\\ C=\left(\left(O_{n}-\Delta_{n}\right)^{2}+\left(O_{p}-\Delta_{p}\right)^{2}\right) / 4 \end{aligned} \tag{7} \]

公式7表明了分类边界是一个圆形。圆心的坐标为\(s_{n}=\left(O_{n}+\Delta_{n}\right) / 2, s_{p}=\left(O_{p}+\Delta_{p}\right) / 2\)，半径为\(\sqrt{C}\)。

此时综合以上公式，在Circle Loss中的超参数为\(O_p,O_n,\gamma,\Delta_p,\Delta_n\)，为了简单起见，简化\(O_p=1+m,O_n=-m,\Delta_p=1-m,\Delta_n=m\)。所以公式7简化为：

\[ \begin{aligned} \left(s_{n}-0\right)^{2}+\left(s_{p}-1\right)^{2}=2 m^{2} \end{aligned}\tag{8} \]

最终决策面被定义为公式8，其中优化目标从\(s_p\rightarrow1,s_n\rightarrow0\)变化为了\(s_p>1-m,s_n<m\)。此时称\(m\)为松弛因子，\(\gamma\)为比例因子。

我觉得对于分类标签样本与配对标签样本还是需要不一样的形式的，这样代码实现起来比较方便。文章里面没有给出最后的损失定义，可能也是这个想法，这里我自己总结了一下，给出最终的损失定义。(当然也有可能作者实现时直接用原本的损失写法)

分类样本损失

\[ \begin{aligned} \mathcal{L}_{\text {circle}}&=\log \left[1+\sum_{j=1}^{L} \exp \left(\gamma \alpha_{n}^{j}\left(s_{n}^{j}-\Delta_{n}\right)\right) \sum_{i=1}^{K} \exp \left(-\gamma \alpha_{p}^{i}\left(s_{p}^{i}-\Delta_{p}\right)\right)\right]\\ \text{Let}\ \ \ \ K&=1,\ \ L=N-1\\ \mathcal{L}_{\text {circle}}&=\log \left[1+\sum_{j=1}^{N-1} \exp \left(\gamma \alpha_{n}^{j}\left(s_{n}^{j}-\Delta_{n}\right)\right) \exp \left(-\gamma \alpha_{p}^{y_i}\left(s_{p}^{y_i}-\Delta_{p}\right)\right)\right]\\ &=-\log \left[\frac{1}{1+\sum_{j=1}^{N-1} \exp \left(\gamma \alpha_{n}^{j}\left(s_{n}^{j}-\Delta_{n}\right)\right) \exp \left(-\gamma \alpha_{p}^{y_i}\left(s_{p}^{y_i}-\Delta_{p}\right)\right)}\right]\\ &=-\log \left[\frac{\exp \left(\gamma \alpha_{p}^{y_i}\left(s_{p}^{y_i}-\Delta_{p}\right)\right)}{\exp \left(\gamma \alpha_{p}^{y_i}\left(s_{p}^{y_i}-\Delta_{p}\right)\right)+\sum_{j=1}^{N-1} \exp \left(\gamma \alpha_{n}^{j}\left(s_{n}^{j}-\Delta_{n}\right)\right)}\right] \end{aligned} \]

这里将相似度变化对比如下图所示：

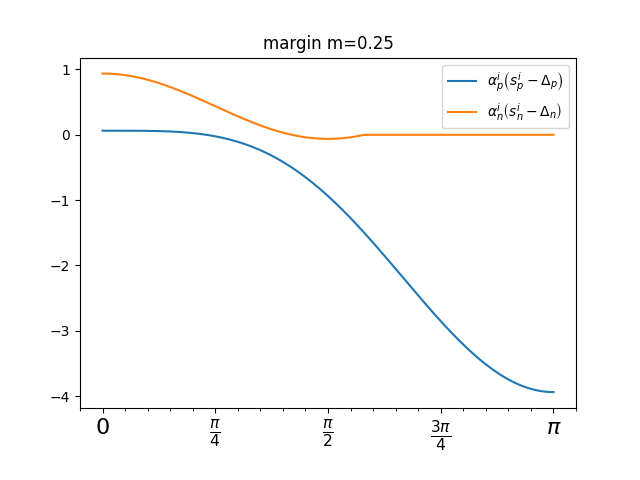
配对标签损失

NOTE 前面提到优化目标为\(s_p\rightarrow1,s_n\rightarrow0\)，实际上不是要求相似度求出来就在\(0\sim1\)内。作者采用cos相似性。对于cos相似性不是要求neg的相似性为-1。因为当你要求A和B的相似性为-1，同时要求A和C的相似性为-1，那么，你就在要求B和C的相似性为 1。所以说，0才是不相似，-1是另一种相似。以上函数中的\([\cdot]_+\)在tensorflow中可以用relu实现。

实验

作者用am-softmax和Circle Loss做了下对比实验，结果如下：

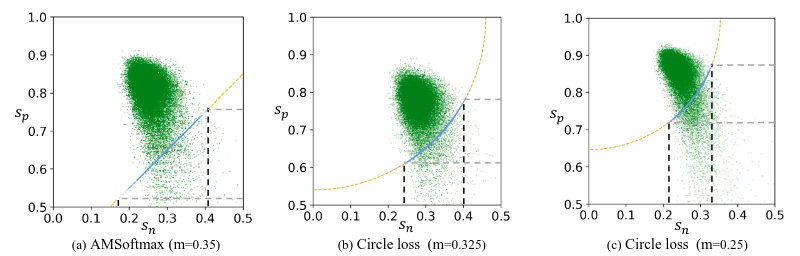
图3：训练收敛后数据分布可视化结果，蓝色点表示训练过程中位于决策边界线的分类相似对，绿色点是收敛后的标记相似对。(a)中am-softmax在训练结束后，相似对的分布比较分散。(b,c)中Circle Loss通过圆形的决策边界，使得相似对聚集到相对集中的区域中。

NOTE 对于别的实验结果我不再赘述，有兴趣的可以自行查看论文。