统计学习方法:支持向量机

这次实现中，关于如何选择违反KKT条件最严重的点在书中没有提到，我首先按照书上的方法实现了一下，但是发现没找到$\epsilon$和违反KKT条件的量化方法，而且只按书上来，实现的SVM效果并不理想。看来我还是没有完全弄透...先写了个初级版的，以后需要再深入了解时可以重温。

支持向量机

原理

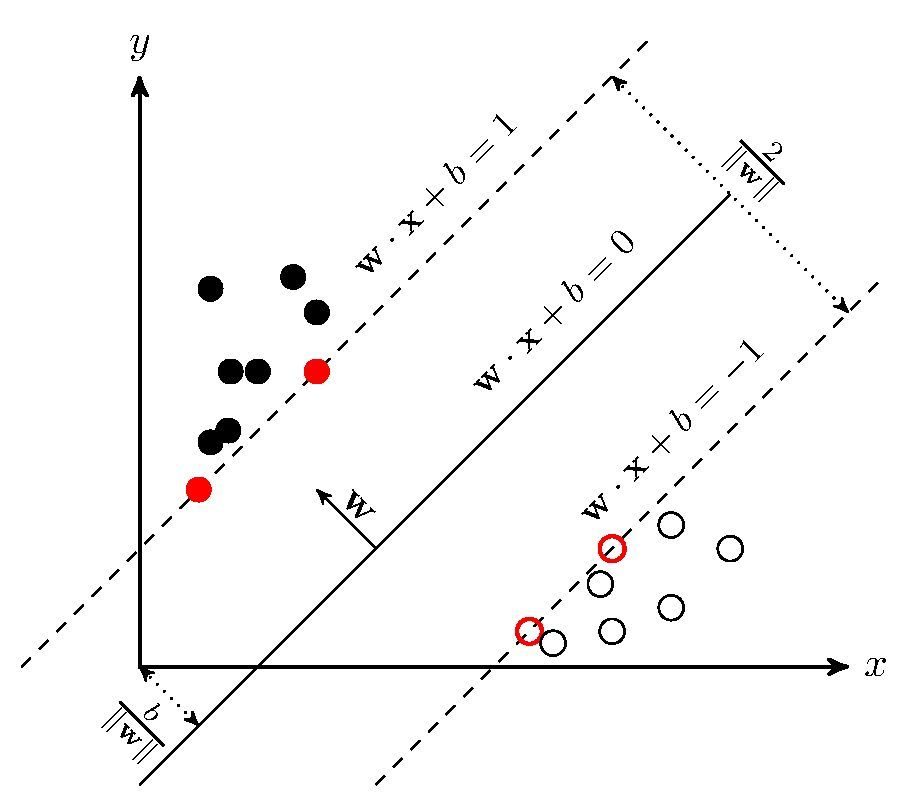
首先我们还是使用感知机中的分类例子,在感知机中分类决策面有无数个,为了找到最优的决策面(人主观地认为能使数据间gap最大的决策面是最好的),提出了最大间隔的线性分类模型.

我们定义分类决策面为$w^Tx+b=0$,任意一点到决策面的距离为$r=\frac{|w^Tx+b|}{||w||}$,对于带标签的数据定义其函数间隔为$r^*=y_i(w^Tx+b)$,几何间隔为$r=\frac{r^*}{||w||}$,对于最大间隔的线性分类模型我们的目标就是最大化所有数据点到决策面的几何间隔: $$\begin{aligned} \max\ &\frac{y_i(w^Tx+b)}{||w||}=\frac{r^*}{||w||}\\ \text{s.t.}\ \ \ &y_i(w^Tx_i+b)\geq r^*,\ i=1,2,...,N \end{aligned}$$

为了求解上述函数的极值,需要做两步:

1. 转换为凸函数

1.1 令$r^*=1$.

因为间隔只是一个尺度,不影响对于$w$的求解.

$$\begin{aligned} \max\ &\frac{1}{||w||}\\ \text{s.t.}\ \ \ &y_i(w^Tx_i+b)\geq 1,\ i=1,2,...,N \end{aligned}$$

1.2 转换为凸函数求最小值(应该是凸优化问题比较便于求解)

$$\begin{aligned} \min\ &\frac{1}{2}||w||^2\\ \text{s.t.}\ \ \ &y_i(w^Tx_i+b)\geq 1,\ i=1,2,...,N \end{aligned}$$

$\frac{1}{2}$是为了便于求导后计算所加的常数项.

2. 求解

2.1 拉格朗日乘数法

先应用拉格朗日乘数法,转换约束条件(如果不理解请参考高等数学第七版下册p118):

$$\begin{aligned} \min_{w,b}\ &\frac{1}{2}||w||^2\\ \text{s.t.}\ \ \ & -y_i(w^Tx_i+b)+1\leq 0,\ i=1,2,...,N \end{aligned}$$

将约束条件逐一带入得到:

$$\begin{aligned} L(w,b,\alpha)=\frac{1}{2}||w||^2+ \sum_{i=1}^N\alpha_i \left[-y_i(w^T x_i+b)+1\right] \end{aligned}$$

2.2 拉格朗日乘对偶形式

根据统计学习方法附录C中关于拉格朗日原始问题的对偶问题中的证明,将上述原始问题转换为对偶形式后得到: $$\max_{\alpha}\ \min_{w,b}\ L(w,b,\alpha)$$

接下来求解过程就变成了先求$\min_{w,b}\ L(w,b,\alpha)$对$w,b$的极小:

$$\begin{aligned} \text{求导并使其为0}\ \ \ \ \frac{\partial }{\partial w}L(w, b, \alpha)&=w-\sum\alpha_iy_ix_i=0\\ \frac{\partial }{\partial b}L(w, b, \alpha)&=\sum\alpha_iy_i=0\\ \\ \text{得到}\ \ \ \ w&=\sum_{i=1}^N \alpha_i y_i x_i\\ \alpha_i& y_i =0\\ \\ \text{带入}\ \ \ \ \min_{w,b}\ L(w, b, \alpha)&=\frac{1}{2}||w||^2+\sum^N_{i=1}\alpha_i(-y_i(w^Tx_i+b)+1)\\ &=\frac{1}{2}w^Tw-\sum^N_{i=1}\alpha_iy_iw^Tx_i-b\sum^N_{i=1}\alpha_iy_i+\sum^N_{i=1}\alpha_i\\ &=\frac{1}{2}w^T\sum^N_{i=1}\alpha_iy_ix_i-\sum^N_{i=1}\alpha_iy_iw^Tx_i+\sum^N_{i=1}\alpha_i\\ &=\sum^N_{i=1}\alpha_i-\frac{1}{2}\sum^N_{i=1}\alpha_iy_iw^Tx_i\\ &=\sum^N_{i=1}\alpha_i-\frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j) \end{aligned}$$

再求上式对于$\alpha$的极大:

$$\begin{aligned} \max_\alpha\ \ \ \ &\sum^N_{i=1}\alpha_i-\frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)\\ \text{再转换为极小问题} &\Downarrow\\ \min_\alpha\ \ \ \ &\frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_i\alpha_jy_iy_j(x_ix_j)-\sum^N_{i=1}\alpha_i\\ \text{s.t.}\ \ \ \ &\begin{cases}\sum^N_{i=1}a_iy_i=0\\a_i\geq 0,\ \ i=1,2,...,N \end{cases} \end{aligned}$$

最后求解时先求解最优的$\alpha$,求得后带入之前公式求解$w,b$.

2.3 SMO算法

最小最优化算法(SMO)是用于求解SVM对偶问题解的。

方法是不断固定其他变量，对两个变量构造二次规划、并通过求出其解析解来优化原始的对偶问题。步骤如下：

1. 检查所有变量$\alpha_1,...,\alpha_N$及对应的样本点$\left( x_{1},y_{1} \right),\ldots,(x_{N},y_{N})$满足KKT条件的情况。
2. 如果均满足KKT条件那么完成训练。
3. 如果有未满足KKT条件的变量，对他们进行优化：
   1. 选择违反KKT条件最严重的样本点，对应的$\alpha_i$作为第一个变量。
   2. 第二个变量$\alpha_j$为对应$|E_i-E_j|$最大的变量，$E_i$为对于输入样本点$x_i$的预测误差。
4. 固定其他变量后，仅对这两个变量进行优化。

2.4 KKT条件

$a_i$与对应样本的$x_i,y_i$的KKT条件为： $$\begin{aligned} \alpha_{i} = 0 &\Leftrightarrow y_{i}g\left( x_{i} \right) \geq 1 \\ 0 < \alpha_{i} < C &\Leftrightarrow y_{i}g\left( x_{i} \right) = 1 \\ \alpha_{i} = C &\Leftrightarrow y_{i}g\left( x_{i} \right) \leq 1 \end{aligned}$$

不满足KKT条件的量化：

1. 计算所有样本点的损失$c=|y_ig(x_i)-1|$
2. 将损失$c$带入上述三个条件中将如果满足，对应的损失置为0
3. 将三个处理后的损失相加，其中的最大值对应的索引就是第一个变量。