Proxy Anchor Loss for Deep Metric Learning论文解读
这是CVPR2020的一篇度量学习的论文.来自韩国.我觉得还蛮有意思的,因此学习一番.
他的图画的是真好看,虽然做的事情其实就是把amsoftmax换个皮...
原理
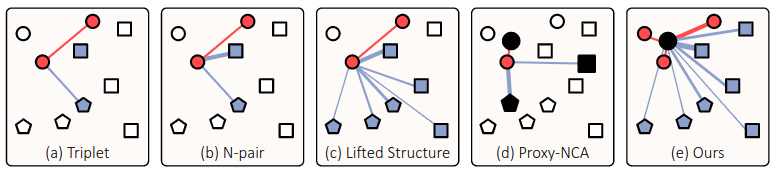
论文主要提出了一个名为Proxy Anchor的损失函数.他相比于上图中a,b,c,d的方法.同时考虑了间距的大小作为损失的系数,且利用了整个batch中所有的数据,并用anchor作为proxy使得聚类中心更加明确.
基于pair的损失
对于一些没有利用整个batch所有数据的方法,那就需要依赖采样来取得triplet pair,N-pair等等,这样实际上引用了额外的复杂度.因此使用基于proxy的方法,不需要pair采样的方式.
基于proxy的损失
基于proxy的度量学习是一种相对较新的方法,可以解决基于pair的损失的复杂性问题。proxy表示训练数据子集的代表,并被估计为嵌入网络参数的一部分。此类别中方法的共同思想是推断一小组的proxy,这些proxy捕获嵌入空间的全局结构,并将每个数据点与proxy相关联,而不是训练过程中的其他数据点。由于proxy的数量明显少于训练数据的数量,因此可以大大减少训练的复杂性.
第一个基于proxy的方法为Proxy-NCA,他使用proxies的Neighborhood Component Analysis作为一种近似,首先为每个类别设置一个proxy,将数据点与proxy关联,拉近正类的距离,拉开负类的距离.
使用proxy有助于极大地提高训练的收敛性,但有一个固有的局限性:由于每个数据点仅与proxy相关联,因此基于pair的方法的丰富的数据间关系不再可用。因此提出Proxy Anchor损失可以克服此问题,因为它的梯度可以反映数据的相对联系,这允许它们的嵌入向量在训练过程中相互影响.
Proxy-NCA Loss
首先介绍原本的损失.Proxy-NCA损失将proxy分配给每个类别,proxy的数量与类别标签的数量相同。给定一个输入数据点作为anchor,将同一类输入的proxy视为正,其他proxy为负。令\(x\)表示输入的嵌入向量,\(p^+\)为正proxy,\(p^-\)为负proxy。损失则为如下:
\[ \begin{aligned} \ell(X) &=\sum_{x \in X}-\log \frac{e^{s\left(x, p^{+}\right)}}{\sum\limits_{p^{-} \in P^{-}} e^{s\left(x, p^{-}\right)}} \\ &=\sum_{x \in X}\left\{-s\left(x, p^{+}\right)+\underset{p^{-} \in P^{-}}{\operatorname{LSE}} s\left(x, p^{-}\right)\right\} \end{aligned} \]
其中\(X\)为整个batch的嵌入向量,\(P^-\)为负proxy的集合,\(s(\cdot,\cdot)\)表示余弦相似度.其中\(\operatorname{LSE}\)为log sum exp.熟悉基于softmax损失的同学应该已经看出来了,这里其实就是交叉熵换了个皮.
对于此损失的梯度如下: \[ \frac{\partial \ell(X)}{\partial s(x, p)}=\left\{\begin{array}{ll} -1, & \text { if } p=p^{+} \\ \frac{e^{s(x, p)}}{\sum\limits_{p^{-} \in P^{-}} e^{s\left(x, p^{-}\right)}}, & \text {otherwise } \end{array}\right. \]
训练时会使得\(x\)与\(p^+\)尽量接近,使得\(x\)与\(p^-\)远离.不过注意到对于正类的梯度是恒定的,对于负类的梯度是有考虑到相似度的.此损失还是比较鲁棒的,但是由于损失仅使每个嵌入向量与proxy相关联,因此它无法利用细粒度的数据间关系。这种缺点限制了通过Proxy-NCA嵌入的能力.
Proxy-Anchor Loss
Proxy-Anchor损失旨在克服Proxy-NCA的局限性,同时保持较低的训练复杂性。主要思想是将每个proxy作为锚,并将其与整个数据批关联,以便在训练过程中数据通过proxy anchor彼此交互。此损失先按照Proxy-NCA的标准设置为每个类别分配一个proxy,公式为:
\[ \begin{aligned} \ell(X)=& \frac{1}{|P+|} \sum_{p \in P^{+}} \log \left(1+\sum_{x \in X_{p}^{+}} e^{-\alpha(s(x, p)-\delta)}\right) \\ &+\frac{1}{|P|} \sum_{p \in P} \log \left(1+\sum_{x \in X_{p}^{-}} e^{\alpha(s(x, p)+\delta)}\right) \end{aligned} \]
这个也是比较老套的设置方法,其中\(\delta\)为margin,\(\alpha\)为尺度系数.将一个batch中所有的嵌入向量\(X\)分成两个子集\(X_p^+,X_p^-\),其中\(X_p^+\)表示proxy\(p\)的正样本嵌入向量,\(X_p^-\)则是剩下的所有向量.
将损失换一个形式: \[ \begin{aligned} \ell(X)=& \frac{1}{\left|P^{+}\right|} \sum_{p \in P^{+}}[\text {Softplus }(\mathop{\operatorname{LSE}}\limits_{x \in X_{p}^{+}} -\alpha(s(x, p)-\delta))] \\ &+\frac{1}{|P|} \sum_{p \in P}\left[\text {Softplus }\left(\mathop{\operatorname{LSE}}\limits_{p \in X_{p}^{-}} \alpha(s(x, p)+\delta)\right)\right] \end{aligned} \]
这样更加符合circle loss中所提出的统一形式了.其中这里的\(|P^+|\)是正样本的统计数量,\(|P|\)是总类别数.这个系数我觉得不加也没关系...
NOTE
我看了下他官方的代码,实际上什么基于proxy的方法就是额外再加一个可训练的聚类中心...我之前的各种损失函数的实现是直接把最后一层作为聚类中心(也就是他们所说的proxy),这么看来把circle loss拉到度量学习的标准任务里肯定也是很能打的.
额外实验1
我做的cifar10分类实现,实际上batchsize改成500之后\(|P^+|\)有99.99的概率为10,\(|P|\)为10。我训练结果只和circle loss差0.8个点。然后我认为删除这个系数没有关系,但结果立马打脸了,差7个点了。其实这个问题还是在于\(\alpha\)系数上面,对于proxy anchor loss和amsoftmax loss来说没有像circle loss中的自适应pace,优化到后期可以说学习率太大也可以说是梯度太大,模型参数波动性会较大。这个实验佐证了自适应pace的重要性。
额外实验2
后面我又做了一下关于\(margin\)的实验,实际上我们考虑softmax分类的过程,要使他分类难度增强应该是降低正确类别的数值,因此应该是\(s_p=cos(\theta_{y_i})-m\),这样才会强制正确类别的向量夹角更小。那么对于不正确的的分类类别,应该是加大他的数值,\(s_n=cos(\theta_{j\neq
y_i})+m\),这样会强制降低向量更加接近垂直。
这里留个小坑,对于circle loss里面的\(margin\)设置我还是得重新仔细看看。
NOTE
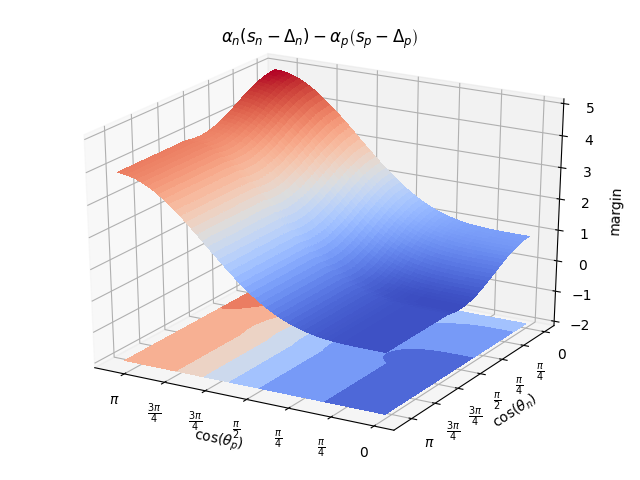
2020-6-23日更新,因为circle loss设置了自定义pace,因此他计算决策面的时候将\(\alpha\)考虑进去了,所以他得到的\(margin\)和我之前设想的不一样。然后我又做了一下他的间距分布图,其实这个损失还是可以继续改进的,大家可以看到当\(\cos(\theta_p)=0,\cos(\theta_n)\in(\pi,\frac{\pi}{2})\)时,对于负pair的损失是较小的。他所说的circle区域实际上是在\(\cos(\theta_p)=0,\cos(\theta_n)=\frac{\pi}{2}\)有一个更小的凹槽,这里是我们的ideal区域。
接下来如果有老哥可以把\(\cos(\theta_p)=0,\cos(\theta_n)\in(\pi,\frac{\pi}{2})\)这块区域的损失重新设计一下,应该可以得到更好的收敛效果。
等等。。这样判断太武断了,应该还需要分析一下梯度的变化。我这里就不继续深入了。