潜在狄利克雷分配模型其实就是一个确定结构的概率图模型，他主要做两件事情:

  1. 学习到话题的单词分布\(p(w|z_k)\),意为给定对应话题得到对应的单词.

  2. 学习到文本的话题分布\(p(z|\mathbf{w}_m)\),意为给定对应文本得到对应的话题.

如下图所示:

  1. \(\varphi_k\sim \text{Dir}(\beta)\)控制了多项分布\(p(w|z_k)\)根据主题随机生成当前文本下的单词分布\(\mathbf{w}\).

  2. \(\theta_{m}\sim \text{Dir}(\alpha)\)控制了多项分布\(p(z|\mathbf{w}_m)\)根据当前文本得到所对应主题的概率分布.

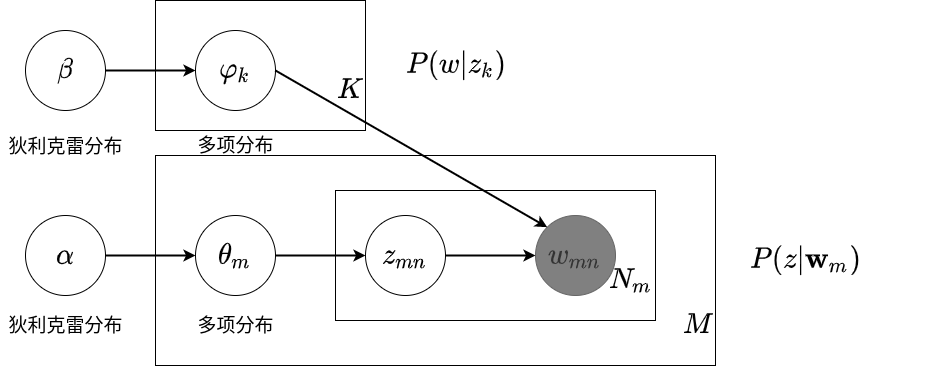
LDA的生成过程

流程见书本图20.3:

  1. 从\(\theta_m\sim Dir(\alpha)\)中随机采样,确定文本的话题分布\(p(z|\mathbf{w}_m)\),这个分布是一个多项分布.
  2. 在文本的话题分布\(p(z|\mathbf{w}_m)\)中采样,一篇文章一共\(N\)个单词,因此采样每个单词对应的\(N\)个主题,即\(z_{mn}\sim p(z|\mathbf{w}_m)\).
  3. 从\(\varphi_k\sim Dir{\beta}\)中随机采样,确定话题的单词分布\(p(w|z_k)\),这个分布也是一个多项分布.
  4. 一共有\(M\)篇文章,每个文章有\(N\)个单词,因此对之前采样得到单词对应的主题\(z_{mn}\)可以在话题的单词分布\(p(w|z_k)\)中采样,代入\(z_{mn}\)后,得到生成的单词\(w_{mn}\).

实际上如果我们生成的整个数据集的单词\(w_{mn}\)恰巧符合于真实的单词分布,那么LDA模型的参数\(\alpha,\beta\)就确定了.

LDA的Gibbs抽样算法

具体推导流程见书本.gibbs抽样的缺点就是效率太低，一个step就需要遍历所有的文本内容，并且需要非常多的step才能进入收敛状态。因此我的代码实现减小了文章个数和特征个数。

LDA的变分EM算法

TODO，此方法效率较高，sklearn中也是使用变分EM进行计算的。太过复杂所以我就没有准备复现。