学习关于polyhedral的基础概念.

What is polyhedral compilation?

reversing a loop nest

for i in range(4):
  a[i] = a[i] + 1
# a[0] = a[0] + 1
# a[1] = a[1] + 1
# a[2] = a[2] + 1
# a[3] = a[3] + 1

如何在不改变边界的情况下修改循环的顺序,我们可以通过修改索引值的方式调整循环的顺序, 定义一个变换函数把索引进行线性映射.

T = lambda i: 4 - 1 - i
for i in range(4):
  a[T(i)] = a[T(i)] + 1
# a[3] = a[3] + 1
# a[2] = a[2] + 1
# a[1] = a[1] + 1
# a[0] = a[0] + 1

我们可以把这个变换函数写成线性函数的形式

# T = a*x + b
T = lambda x: -x + 3

can we reverse this loop?

我们可以反转这个循环到另一个吗? 显然不可以,因为他们的改变顺序后,代码的实际执行的结果变了.

for i in range(1,4):
  x[i] = x[i-1]
#     |
#     V
for i in range(3,0,-1):
  x[i] = x[i-1]

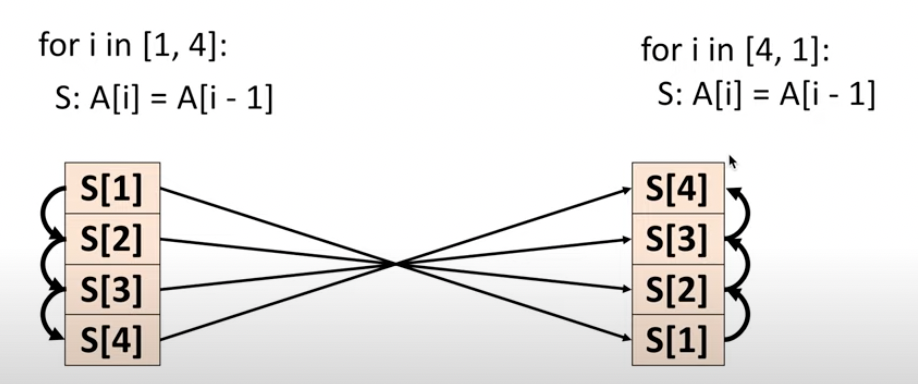
多面体编译的思想即: 1. 取现有的loop nest 2. 决定需要reorder的迭代位置 3. 提出一个线性函数进行映射到你需要的循环顺序 4. 映射并得到一个新的loop nest

A little more formalism

对于上述的两种循环,可以对statements的区域进行定义, 首先他们的循环范围都是一致的.但是他们每一个statement的执行点不同,比如逆循环时,x[4]其实是在最前面执行.

我们定义entry为发生的时间:

\[ \begin{aligned} &for\ i\ in\ [1,4]:\ \ &\text{range:} \ \{x[i]\ \in \ 1 \leq i \leq 4\}\\ &\ \ x[i] = x[i-1] & \text{entry}\ \ \{x[i] \rightarrow i \} \ \ \text{x[i] 在 i 时刻被执行} \\ & & \\ &for\ i\ in\ [4,1]:\ \ &\text{range:} \ \{x[i]\ \in \ 1 \leq i \leq 4\}\\ &\ \ x[i] = x[i-1] & \text{entry}\ \ \{x[i] \rightarrow 5-i \} \ \ \text{x[i] 在 5-i 时刻被执行}\\ \end{aligned} \]

接下来我们定义数据依赖:一个statement pair \((a \rightarrow)\)表示, 声明a将发送数据到声明b. 那么对于第一个序列的数据依赖如下,对于第一个序列的数据依赖如下, 即每个时间点下, 存在着\(x[i+1]\)依赖\(x[i]\).

\[ \begin{aligned} \text{dep:}\ \ &\{(x[i]\rightarrow x[i+1]) \in 1 \leq i \leq 3 \} \end{aligned} \]

然后我们来构造一组违法依赖的情况,即本来\(i\)是先于\(i+1\)发生,如果在经过schedule经过线性变化之后, \(i\)发生的时间反而大于等于\(i+1\)发生的时间,那么就表示当前依赖被破坏了.

\[ \begin{aligned} \text{invalid dep:}\ \ &\{x[i]\rightarrow x[i+1] \in entry(i) \geq entry(i+1) \} \end{aligned} \]

把违法数据依赖的限制条件,和原始的数据依赖集合做交集 (意思是只要满足当前限制条件的数据,都是违反数据依赖的无效变化数据):

\[ \begin{aligned} \ \ &\{x[i]\rightarrow x[i+1] \in 1 \leq i \leq 3 \ \land (entry(i) \geq entry(i+1))\} \end{aligned} \]

此时我们的entry为5-i那么代入依赖中得到: \[ \{x[i]\rightarrow x[i+1] \in 1 \leq i \leq 3 \ \land 5-i >= 5-(i+1)\} \]

很明显,可以发现上述公式的可行解范围为\(1 \sim 3\), 那么表示在所有的数据取值中,都会违反数据依赖,所无效的变换.

Integer Linear Programming and Lexicographic Order

上一节中我们知道了如何检查线性变换之后的有效性, 如何把这个过程更加通用和泛化?

Integer Linear Programming (ILP)

整数线性规划问题就是专门解决线性变换下的不等式求解问题的.比如我们需要求解(中间不能出现非线性函数,出现两个变量互相作用,):

\[ \begin{aligned} 3 x + 4y +7 \geq 0 \\ -3 x - 3 \leq 0 \end{aligned} \]

这些问题其实是NP-Hard问题,并且有可能同时需要解决上百个变量的情况

Lexicographic Order

词典顺序定义成一种\(>>\)或者\(<<\)的形式, 他的机制类似于: \[ \begin{aligned} [a,b] >> [c,d] == \left(a>c\ ||\ (a==c \ \&\&\ b > d)\right) \end{aligned} \]

同时要检查他的正确性, 我们需要利用ILP solver多重递归的解析每个分支的有效性.

多个维度下的线性变换问题

for i in range(1,4):
  for j in range(1,3):
      A[i][j] = A[i-1][j+1]

此时如果我们交换i和j的循环顺序.

polyhedral入门学习