背景

Egg是一个基于EGraph的程序优化框架, 作者在其中实现基于Equality Saturation概念的优化方法, 简单来说就是通过将所有的表达式保存在EGraph这个数据结构中,可以按任意顺序实施RBO(基于规则的优化), 因为其中同时存储了所有可能的表达式, 所以没有传统优化中phase ordering的问题, 最终可通过CostModel提取出最优的图结构.

Egg在编译优化方面已经有许多应用了, 比如王润基大佬写的SQL 优化器, 其中也详细解释了Egg的使用, 不了解的朋友可以参考一下.

在端侧AI编译中,每个阶段都需要大量的优化与trade-off, 比如中端的计算图优化与后端的算子Fusion以及后端算子的量化类型(平衡精度/速度), 如果基于传统优化方式, 可能许多模型最优的Pass顺序,算子Fusion方案都需要编译器工程师手动调试与指定. 这主要就是因为传统优化方式一旦lower之后就丢失了之前的信息, 失去了最优的可能性, 因此考虑采用Equality Saturation技术来将中端优化/后端Fusion/Tiling/算子精度选择都放入其中进行整体性优化,希望可以得到尽量优化的编译结果.

Egg中Cost累积机制带来的问题

问题描述

不论是中端优化还是后端Fusion, 都会涉及到算子的折叠与合并. 通常无分支的算子的合并, 那么合并后Cost必然减小, 可以自然的选择当前Cost最小的表达式. 但是如果多分支的情况下就会遇到问题.

假设我们导入的模型有卷积/激活等算子,在Cpu上我们支持的Relu6/Clamp算子,他们的Cost分别为60,70. 后端支持卷积Conv,通用激活Act,以及卷积+通用激活ConvAct, 设他们的Cost分别为100,50,125. 其中执行ConvAct肯定是快于分别执行Conv和Act.

考虑如下的模型结构:

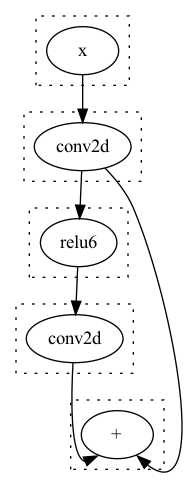
同时我们的存在这样一个Rule : rw!("fold_conv_act"; "(act (conv2d ?x))" => "(conv2dAct ?x)"), 在经过Egg的Runner实施优化后, 得到了这样的结果:

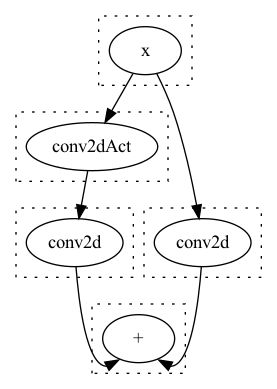
大家可以发现, 虽然我们合并了一个Act, 但是反而多计算了一次Conv, 最终的计算时间增加了.

探究原因

Egraph中保存了展平的数据结构, 对于每一个Eclass选择其内部最小Cost的ENode来作为它的Cost. 但是因为EGraph中找不到入口点, 所以是反复遍历所有的EClass, 直到每个Eclass不再减小时退出.

其核心逻辑如下:

    let mut did_something = true;
    while did_something {
        did_something = false;

        for class in self.egraph.classes() {
            let pass = self.make_pass(class);
            match (self.costs.get(&class.id), pass) {
                (None, Some(new)) => {
                    self.costs.insert(class.id, new);
                    did_something = true;
                }
                (Some(old), Some(new)) if new.0 < old.0 => {
                    self.costs.insert(class.id, new);
                    did_something = true;
                }
                _ => (),
            }
        }
    }
.
.
.
fn make_pass(&mut self, eclass: &EClass<L, N::Data>) -> Option<(CF::Cost, L)> {
    let (cost, node) = eclass
        .iter()
        .map(|n| (self.node_total_cost(n), n))
        .min_by(|a, b| cmp(&a.0, &b.0))
        .unwrap_or_else(|| panic!("Can't extract, eclass is empty: {:#?}", eclass));
    cost.map(|c| (c, node.clone()))
}

问题就在于make_pass的时候他无法得到上下文的信息, 如下图所示:

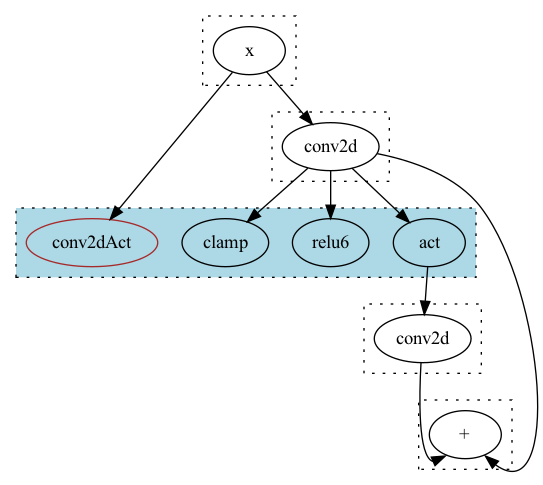
在蓝色的EClass中它自然会选择当前的conv2dAct节点,因为它是当前Eclass最小Cost的ENode.

可能的解决方案

下面写两个我思考的方案, 也欢迎大家在评论区一起讨论.

方案1

简单的方案可以在编写rule的时候判断要折叠的算子的user个数,如果是会引起这种现象的情况, 就不进行折叠. 不过这样总觉得和Equality Saturation的思路相悖, 不是一个很完美的做法.

方案2

需要记录每个ENode可能的Compute Sequence, 如同上图所展示的那样, 比如对于Add节点左边可能存在x -> conv2d -> relu6 -> conv2d, x -> conv2dAct -> conv2d等4种情况,右边则只有x -> conv2d一种情况, 然后消除两边计算序列的交集, 从而算得正确的cost值. 不过这样存储的Compute Sequence在每经过一个EClass时,都是按EClass.Nodes.Count来翻倍的, 需要一种节省内存的数据结构. 同时因为计算Cost的时候是将所有表达式展平之后处理的, 还需要方便的从中间节点进行替换. 总之不是一个容易实现的方案.

附录

最小的复现代码NN.rs, 可以放在egg/tests目录下运行:

use egg::{rewrite as rw, *};
use ordered_float::NotNan;

pub type EGraph = egg::EGraph<NeuralNetwork, ()>;
pub type Rewrite = egg::Rewrite<NeuralNetwork, ()>;

pub type Constant = NotNan<f64>;

define_language! {
    pub enum NeuralNetwork {
        "+" = Add([Id; 2]),
        "-" = Sub([Id; 2]),
        "*" = Mul([Id; 2]),
        "/" = Div([Id; 2]),
        "conv2d" = Conv2D(Id),
        "act" = Act(Id),
        "relu6" = Relu6(Id),
        "clamp" = Clamp(Id),
        "conv2dAct" = Conv2DAct(Id),
        Constant(Constant),
        Symbol(Symbol),
    }
}

pub struct CostFn<'a> {
    pub egraph: &'a EGraph,
}

impl egg::CostFunction<NeuralNetwork> for CostFn<'_> {
    type Cost = f32;
    fn cost<C>(&mut self, enode: &NeuralNetwork, mut costs: C) -> Self::Cost
    where
        C: FnMut(Id) -> Self::Cost,
    {
        // let id = &self.egraph.lookup(enode.clone()).unwrap();
        let mut costs = |i: &Id| costs(*i);
        let op_cost = match enode {
            NeuralNetwork::Conv2D(..) => 100.0,
            NeuralNetwork::Act(..) => 50.0,
            NeuralNetwork::Relu6(..) => 60.0,
            NeuralNetwork::Clamp(..) => 70.0,
            NeuralNetwork::Conv2DAct(..) => 125.0,
            _ => 1.0,
        };
        let c = enode.fold(op_cost, |sum, id| sum + costs(&id));
        c
    }
}

#[rustfmt::skip]
pub fn rules() -> Vec<Rewrite> { vec![
  rw!("fold_conv_act";  "(act (conv2d ?x))" => "(conv2dAct ?x)"),
  rw!("relu6_to_clamp";  "(relu6 ?x)" => "(clamp ?x)"),
  rw!("relu6_to_act";  "(relu6 ?x)" => "(act ?x)")
]}

#[test]
fn duplicte_branch_select() {
    let expr: RecExpr<NeuralNetwork> = "(+ (conv2d x) (conv2d (relu6 (conv2d x))))"
        .parse()
        .unwrap();
    let mut egraph = EGraph::default();
    egraph.add_expr(&expr);
    egraph.dot().to_dot("target/pre.dot").unwrap();

    let runner: Runner<NeuralNetwork, ()> = Runner::default().with_expr(&expr).run(&rules());

    let extractor = Extractor::new(&runner.egraph, AstSize);
    runner.egraph.dot().to_dot("target/graph.dot").unwrap();

    let (best_cost, best_expr) = extractor.find_best(runner.roots[0]);
    println!("End ({}): {}", best_cost, best_expr.pretty(80));
    let mut egraph = EGraph::default();
    egraph.add_expr(&best_expr);
    egraph.dot().to_dot("target/post.dot").unwrap();
}

Equality Saturation优化在AI编译器中遇到的挑战

Equality Saturation优化在AI编译器中遇到的挑战

背景

Egg中Cost累积机制带来的问题

问题描述

探究原因

可能的解决方案

方案1

方案2

附录