Alibaba EasyDist 浅析

对于阿里巴巴开源的EasyDist: Automated Parallelization System and Infrastructure for Multiple Ecosystems代码解读, 主要关注IR设计与搜索域构造.

整体流程

主要核心为4步, 预处理, 切分标注, 图转换, 构造约束模型并求解.

def easydist_shard(fx_module: torch.fx.GraphModule, state_tensor_num, *args, **kwargs):

    # (1) preprocess pass
    fx_module = preprocess_traced_graph(fx_module)

    if mdconfig.log_level <= logging.DEBUG:
        fx_module.print_readable()

    # (2) sharding annotation
    with _sharding_ann_env():
        start_t = time.perf_counter()
        sharding_interpreter = EDTorchShardingAnn(fx_module)
        flatten_args = tree_flatten_spec(list(args) + list(kwargs.values()), fx_module._in_spec)
        sharding_info, shape_info = sharding_interpreter.run(*flatten_args)
        logger.info(f"[EDTorchShardingAnn.time]:\t {time.perf_counter() - start_t} s.")
        if mdconfig.log_level <= logging.DEBUG:
            rich.print("sharding_info:\n", sharding_info)
            rich.print("shape_info:\n", shape_info)

    # sync sharding info for all process
    torch.distributed.broadcast_object_list(sharding_info, src=0, device="cuda")

    # (3) translate fx.GraphModule into MetaGraph
    meta_graph = torch2meta_graph(fx_module, state_tensor_num, sharding_info, shape_info)
    meta_graph.dump()

    if mdconfig.log_level <= logging.DEBUG:
        rich.print(meta_graph)

    # (4) construct AutoFlowSolver and run ILP
    device_mesh = get_device_mesh()
    device_mesh_shape = (device_mesh.size(0), device_mesh.size(1))

    total_memery = torch.cuda.get_device_properties(torch.cuda.current_device()).total_memory
    solver = AutoFlowSolver(device_mesh_shape, total_memery=total_memery)

    if mdconfig.enable_graph_coarsen:
        logger.info(f"enable graph coarsen with level {mdconfig.coarsen_level}.")
        solver.add_coarsen_graph(meta_graph)
    else:
        solver.add_graph(meta_graph)

    start_t = time.perf_counter()
    if mdconfig.enable_graph_coarsen:
        opt_strategy = solver.ilp_solve()
    else:
        opt_strategy = solver.ilp_optimize()
    logger.info(f"[AutoFlowSolver.time]:\t {time.perf_counter() - start_t} s.")

    if mdconfig.log_level <= logging.DEBUG:
        rich.print(opt_strategy)

    sharding_strategies = get_torch_sharding_strategy(fx_module, opt_strategy)

    if mdconfig.log_level <= logging.DEBUG:
        rich.print(sharding_strategies)

    return shape_info, meta_graph, opt_strategy, sharding_strategies

切分标注

首先引入切分的数据结构:

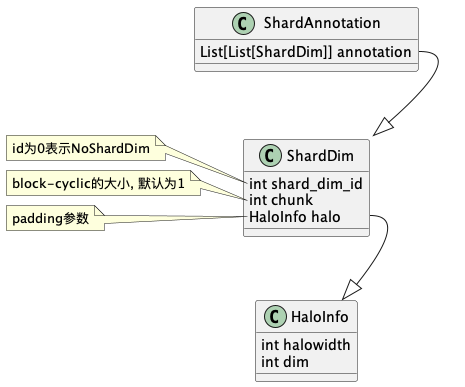
这里ShardDim表示的是先chunk划分再切分的逻辑,比如[1, 1, 2, 2]可以先划分两块(chunk)-> [1, 1] and [2, 2],再切分(shard)-> [1, 2] | [1, 2]. 使用一维数组[ShardDim]表示一个输入参数所对应的切分, 多个输入时得到类似[[ShardDim], ...]的二维数组, 因此ShardAnnotation就是使用二维数组来存储切分信息, 来表示一个操作的切分输入切分信息.

假设一个在两个gpu上运行的简单的小网络:

class Net(nn.Module):
    def __init__(self, *args, **kwargs) -> None:
        super().__init__(*args, **kwargs)
        self.fc = torch.nn.Linear(32*32*3, 64, False)

    def forward(self, x: torch.Tensor):0
        v0 = torch.flatten(x, 1) # 128,32*32*3
        v1 = self.fc(v0)
        return v1

以上计算的计算图如下:

class <lambda>(torch.nn.Module):
    def forward(self, arg0, arg1, arg2, arg3, arg4):
        arg0_1: f32[64, 3072], arg3_1, arg3_2: f32[128, 3, 32, 32], = fx_pytree.tree_flatten_spec([arg0, arg1, arg2, arg3, arg4], self._in_spec)
        # No stacktrace found for following nodes
        view: f32[128, 3072] = torch.ops.aten.view.default(arg3_2, [128, 3072]);  arg3_2 = None
        t: f32[3072, 64] = torch.ops.aten.t.default(arg0_1)
        mm: f32[128, 64] = torch.ops.aten.mm.default(view, t);  view = t = None
        return pytree.tree_unflatten([arg0_1, None, mm], self._out_spec)

通过一个继承了torch fx的Interpreter的类EDTorchShardingAnn来解释执行整个图, 一边执行一遍获取修改. 对于不同的节点类型, 执行不同的visitleaf函数:

1. placeholder

placeholder对应的应该输入节点, 如果检查到当前节点没有sharding annotation以及combination annotation, 那么会进入preset_meta_spmd函数进行统一处理.

preset_meta_spmd函数通过不同的op类型分发到不同的rule中进行获取.

def preset_meta_spmd(meta_op, input_args=None):
    if isinstance(meta_op, str):
        args, kwargs = input_args
        return PresetMetaSPMD.op_rules[meta_op](args, kwargs)
    elif meta_op.name in PresetMetaSPMD.op_rules:
        if input_args is None:
            args, kwargs = meta_op.input_args
        else:
            args, kwargs = input_args
        return PresetMetaSPMD.op_rules[meta_op.name](args, kwargs)
    return None, None

对于placeholder则进入meta_spmd_placeholder函数进行处理, 这里也是使用了统一的view_propagation函数构造sharding annotation以及combination annotation.

def meta_spmd_placeholder(args, kwargs):
    input_shape = args.shape
    output_shape = args.shape

    view_ann = view_propagation(input_shape, output_shape, world_size=device_mesh_world_size())
    return view_ann['sharding_ann'], view_ann['combination_ann']

view_propagation的过程比较复杂, 但是对于输入shape和输出shape相同的节点来说还是比较简单的. 他这里会首先构造[[NoShardDim]* ShapeRank]作为sharding annotation, 比如输入shape为[128, 3, 32, 32], 那么构造出[[NoShardDim, NoShardDim, NoShardDim, NoShardDim]]表示全部不切分. 然后遍历每个维度, 如果当前维度大于world size(所有并行度), 则表示可以切分, 那么就构造一个ShardDim(id++), 对于这个例子将会构造出[[ShardDim(1), NoShardDim, NoShardDim, NoShardDim]].

2. call_function

在visit call_function时, 构造出MetaOp后再使用meta_exec去执行. 然后检查是否有sharding_ann, combination_ann的cache,如果没有那么使用preset_meta_spmd来构造.

args, kwargs = materialize_args_kwargs(args_meta, kwargs_meta)
meta_op = MetaOp(func=target,
                  input_args=(args, kwargs),
                  shard_size=device_mesh_world_size(),
                  name=ops_name)
# user fake tensor here, maybe use shape/dtype info from `make_fx`
meta_out = meta_op.meta_exec(flat_meta_input=pytree.tree_flatten((args_meta,
                                                                  kwargs_meta))[0])
.
.
.
sharding_ann, combination_ann = preset_meta_spmd(meta_op, (args_meta, kwargs_meta))

对于expand来说, 并没有对应的切分信息构造, 所以他的sharding_ann为[[NoShardDim, NoShardDim, NoShardDim]]. 对于view, sharding_ann也是通过view_propagation来构造的. 对于矩阵乘, 通过meta_bmm来构造标注, 此时构造标注时除了需要检查是否可以切分, 同时还需要匹配切分的维度, 比如这里两个输入的batch维度使用相同的id, 矩阵的k维度用相同的id: ShardAnnotation([[ShardDim(1), ShardDim(2)], [ShardDim(2), ShardDim(3)]])

在preset_meta_spmd中, 也有一些算子没有添加对应的rule, 所以此时就进入meta_op.sharding_discovery构造对应的shard annotation. 比如对于torch.ops.aten.t.default算子, 会在sharding_discovery中调用_try_sharding(self, fixed_annotation, subsequence_annotation, global_output, start_dim=0)函数获得对应的shard annotation. _try_sharding是一个递归的函数, 第一次进入时fixed_annotation=ShardAnnotation([]), subsequence_annotation=ShardAnnotation([[NoShardDim, NoShardDim]]). 然后在其中遍历所有的输入shape dim,逐一修改原始的subsequence_annotation[0], 获得try_annotation, 然后再进入_try_sharding.

for dim in range(start_dim, len(subsequence_annotation[0])):
    if subsequence_annotation[0][dim].shard_dim_id != 0:
        continue
    try_annotation = copy.deepcopy(subsequence_annotation[0])
    try_annotation[dim] = ShardDim.get_shard_dim(shard_dim_id_flag)
    self._try_sharding(fixed_annotation + ShardAnnotation([try_annotation]),
                        subsequence_annotation[1:], global_output)

再次进入时此时shard annotation的subsequence为空, 首先使用当前的fixed_annotation执行self.exec, 获得切分过的sharded_output. 对于这个转置操作, 原本的输出为torch.Size([3072, 64]), 而在fixed_annotation=ShardAnnotation([[ShardDim(1), NoShardDim]])的条件下则获得到[torch.Size([3072, 32]),torch.Size([3072, 32])](转置操作的输入切分在dim 0上,则输出切分在dim 1上).

进入try_combination(sharded_output, global_output)函数, 这里输入只有一个tensor, 所以进入try_combination_single, 他这里的逻辑就是遍历三种组合函数['try_combination_identity','try_combination_reduce', 'try_combination_gather'], 找到当前所需要的, 显然这个例子中尝试成功后得到的combination_func为functools.partial(<function CombinationFunc.gather at 0x7f5bd501f0d0>, dim=1). 因为将sharded_output gather就可以还原到global_output.

def try_combination_single(sharded_output_, global_output_):
    # check all sharded tensor have equal dimension of global_output
    for sharded_tensor in sharded_output_:
        if len(sharded_tensor.shape) != len(global_output_.shape):
            return None

    for func_name in TRY_COMBINATION_FUNC:
        combination_func = TRY_COMBINATION_FUNC[func_name](sharded_output_, global_output_)
        if combination_func:
            return combination_func

    return None

if len(subsequence_annotation) == 0:
    try:
        sharded_output = self.exec(shard_annotation=fixed_annotation,
                                    priority_shard_dim_id=shard_dim_id_flag)
    except RuntimeError as e:
        logger.debug(f"[{fixed_annotation}] {e}")
        return
    except:
        logger.debug(f"[{fixed_annotation}] run op.exec failed")
        return

    haloinfo = None
    combination_func = try_combination(sharded_output, global_output)
    .
    .
    .
    if combination_func is not None and not isinstance(combination_func, HaloHint):
        self.__combination_ann[shard_dim_id_flag] = combination_func
        # inject haloinfo
        fixed_annotation.inject_haloinfo(haloinfo, shard_dim_id_flag)

        self.__sharding_annotion = copy.deepcopy(fixed_annotation)
        self.__find_new_strategy = True
    else:
        logger.debug(f"[{fixed_annotation}] combination failed")
    return

图转换

这里需要先描述一下meta ir的数据结构: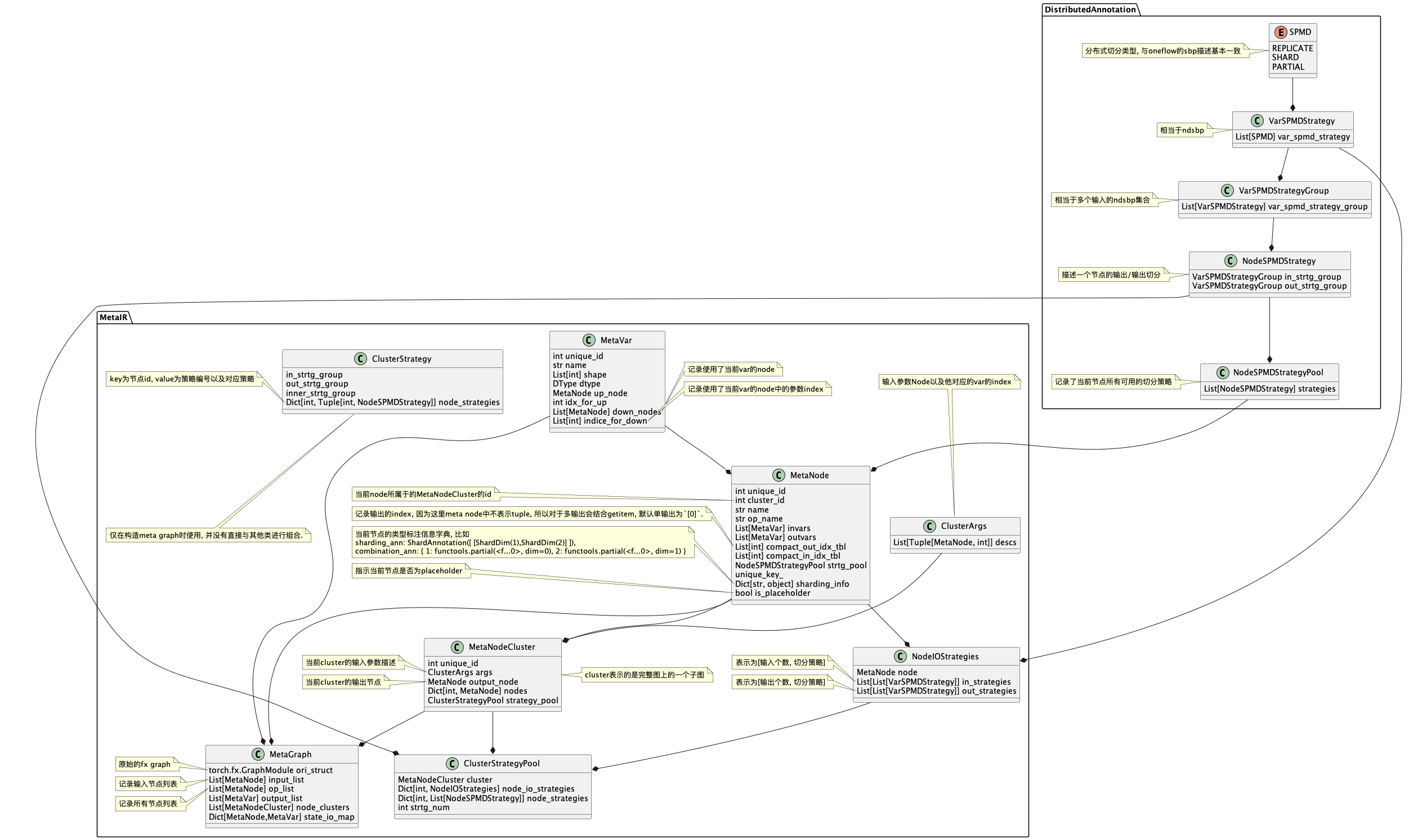

在torch2meta_graph(fx_module: torch.fx.GraphModule, state_tensor_num, sharding_info, meta_info)函数中将原本的带有sharding annotation的fx graph转换为meta的graph, 同时将sharding info也转换为torch的SPMD表示. 具体流程如下:

1. 构造meta_graph
2. 遍历fx_module中所有的节点, 根据节点类型进行处理(每个fx graph的输出节点除了list/tuple都构造MetaVar, 除了getitem都构造MetaNode)

• call_function
  1. 构造MetaVar, 此时metavar表示为当前call的输出, MetaVar(name=node.name, shape=meta_info[node.name]["shape"], dtype=ABSTRACT_DTYPE[meta_info[node.name]["dtype"]])
  2. 构造MetaNode, 此时outvars为当前的MetaVar, invars为空.
  3. 记录Node到MetaGraph的Nodes中
• placeholder或者get_attr
  1. 构造MetaVar, 同上.
  2. 构造MetaNode, MetaNode(name=node.name,op_name=node.op,invars=[],outvars=[meta_var],sharding_info=node_sharding_info,is_placeholder=True)
  3. 记录Node到MetaGraph的Nodes和Inputs中
• output
  1. 获取output_names

3. 重新遍历fx module中的所有节点, 更新MetaNode和MetaVar的连接关系

• call_function
  1. 遍历当前call function对应的MetaNode的输入参数
  2. 对于如果输入参数存在对应的MetaVar, 那么对调用meta_node.set_in_var(in_var, idx)来更新当前meta_node中的invars

4. 根据output_names把对应的meta var添加到meta graph中
5. 构造state_io_map, 遍历state_tensor_num, 将输入的node映射到输出的var上
6. 调用graph.coarsen函数来构造clusters, 这里根据不同的级别选择不同的构造方式, 默认使用build_cone_clusters函数来构造:
   1. 遍历所有节点, 收集所有的cone root
      • 如果节点有多个下游节点或者没有下游节点,那么作为cone root.
      • 如果只有一个下游节点时, 有多个上游节点也是cone root, 有一个上游节点时则需要判断数据量, 如果输出数据量小于输入数据量那么也是cone root
   2. 获取所有cone roots的id, 得到root_ids.
   3. 遍历所有的cone roots构造Cluster
      • 构造MetaNodeCluster(unique_id=cluster_id), 其中cluster_id自动递增
      • 调用build_cone_cluster(cone_root, root_ids, cluster)填充cluster.
        1. 将当前root添加到当前cluster中cluster.add_node(cone_root), 此时设定root node的cluster id
        2. 遍历当前cone root的输入节点, 如果当前节点不在之前收集的cone roots中,那么递归的调用build_cone_cluster(up_node, root_ids, cluster)填充cluster
      • 调用finalize函数
        1. 确定当前cluster的args和output node
        2. 为当前cluster构造ClusterStrategyPool(self)
        3. 获取输出节点的out_strtg_pool NodeSPMDStrategyPool,
           • 如果当前节点存在strtg_pool的属性那么直接返回
           • 否则通过sharding_info进行构造
           • 首先遍历shard ann, 将每一个可切分的维度都构造出一个NodeSPMDStrategy(这里构造则是将ShardDim的表示转换为SPMD的表示)
           • 比如对于一个[[ShardDim(1), ShardDim(2)]]的shard ann 将构造出三组切分策略NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([SHARD({'dim': 0})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([SHARD({'dim': 0})])])), NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([SHARD({'dim': 1})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([SHARD({'dim': 1})])])), NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE])]))
           • 然后再因为当前的DEVICE_MESH_1D==0, 再将每个NodeSPMDStrategy都进行扩展REPLICATE得到类似NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])]))
           • 这里我设置的gpu个数为两个, 但是实际上获取到的device mesh为(1,2), 所以应该是为了保证sbp的个数应该和拓扑结构的维度相同, 所以需要扩展VarSPMDStrategy的维度.
        4. 遍历out_strtg_pool
           1. 构造ClusterStrategy cluster_strtg
           2. 给cluster_strtg设置当前的node_strategy
           3. 使用back_build_strategy将当前的策略反向更新到cluster的其他节点
           4. 将当前cluster_strtg添加到strategy_pool中

最终得到的meta graph的一部分如下, 总的来说就是将原图中的节点转换为MetaNode以及MetaVar, 然后根据一定的策略划分出MetaNodeCluster的子图, 接下来对每个Cluster中的所有Node添加一系列的切分候选集:

=====================
[MetaIR]

input_list: [arg0_1, arg2_1, arg3_3, arg3_4]

[arg0_1] <--- [placeholder] --- []
[arg2_1] <--- [placeholder] --- []
[arg3_3] <--- [placeholder] --- []
[arg3_4] <--- [placeholder] --- []
[view] <--- [torch.ops.aten.view.default] --- [arg3_3]
[t] <--- [torch.ops.aten.t.default] --- [arg0_1]
[mm] <--- [torch.ops.aten.mm.default] --- [view, t]
[_log_softmax] <--- [torch.ops.aten._log_softmax.default] --- [mm]
[getitem, getitem_1] <--- [torch.ops.aten.nll_loss_forward.default] --- [_log_softmax, arg3_4]
[ones_like] <--- [torch.ops.aten.ones_like.default] --- [getitem]
[nll_loss_backward] <--- [torch.ops.aten.nll_loss_backward.default] --- [ones_like, _log_softmax, arg3_4, getitem_1]
[_log_softmax_backward_data] <--- [torch.ops.aten._log_softmax_backward_data.default] --- [nll_loss_backward, _log_softmax]
[t_1] <--- [torch.ops.aten.t.default] --- [_log_softmax_backward_data]
[mm_1] <--- [torch.ops.aten.mm.default] --- [t_1, view]
[t_2] <--- [torch.ops.aten.t.default] --- [mm_1]
[t_3] <--- [torch.ops.aten.t.default] --- [t_2]
[mul_] <--- [torch.ops.aten.mul_.Tensor] --- [arg2_1]
[add_] <--- [torch.ops.aten.add_.Tensor] --- [mul_, t_3]
[add__1] <--- [torch.ops.aten.add_.Tensor] --- [arg0_1, add_]

output_list: [add__1, add_, getitem]
=====================

node clusters:
cluster id: 0
  nodes: arg0_1, 
  inputs: [[arg0_1, 0]]
  output: arg0_1
strategies:
node strategies: 
{
1: [NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, REPLICATE])]))],
}
node io strategies: 
{
1: arg0_1
in strategies: [[VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})]), VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})]), VarSPMDStrategy([REPLICATE, REPLICATE])]]
output strategies: [[VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})]), VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})]), VarSPMDStrategy([REPLICATE, REPLICATE])]],
}
cluster id: 1
  nodes: arg3_4, 
  inputs: [[arg3_4, 0]]
  output: arg3_4
strategies:
node strategies: 
{
7: [NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, REPLICATE])]))],
}
node io strategies: 
{
7: arg3_4
in strategies: [[VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})]), VarSPMDStrategy([REPLICATE, REPLICATE])]]
output strategies: [[VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})]), VarSPMDStrategy([REPLICATE, REPLICATE])]],
}
cluster id: 2
  nodes: view, arg3_3, 
  inputs: [[arg3_3, 0]]
  output: view
strategies:
node strategies: 
{
9: [NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, REPLICATE])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, REPLICATE])]))],
5: [NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 0})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})])]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, SHARD({'dim': 1})])])),
    NodeSPMDStrategy(in_strtg_group: VarSPMDStrategyGroup([]), out_strtg_group: VarSPMDStrategyGroup([VarSPMDStrategy([REPLICATE, REPLICATE])]))],
}
.
.
.

约束模型与求解

这里使用mip构造了一个约束模型, 对于enable_graph_coarsen的配置下, 会进入add_coarsen_graph来将meta graph转换为约束模型. 在这个函数中遍历所有meta graph中的cluster执行add_cluster.

具体看一下add_cluster: 1. 获取cluster的strtg_pool 2. 遍历pool中的切分策略, 为每个切分策略构造出一个对应的binary var, 来表示是否选择这个切分. 3. 使用对应的pool与pick vars构造出mip_info = ClusterMipInfo(cluster, cluster_strtg_pool, mip_vars) 4. 遍历当前cluster的args进行加边self.add_cluster_edge(var, input_idx, down_node=input_node) 1. 对于一个有上下连接关系的cluster,需要进行加边 2. 获取他的输入node的outvar的切分策略up_out_strategy_list,获取他输出node的invar切分策略候选down_in_strategy_list 3. 构造出[up_out_strategy_list,down_in_strategy_list]大小的mip binary var矩阵, 用于标记每个连接是否选择 4. 再计算[up_out_strategy_list,down_in_strategy_list]大小的通信开销矩阵, 也就是对于每个切分的组合计算额外的通信开销 5. 再计算[up_out_strategy_list,down_in_strategy_list]大小的内存开销矩阵 5. 开始ilp_solve 1. 添加约束目标, 初始化comm_cost, mem_cost, 再遍历所有的cluster edge进行update 2. comm_cost += mip.xsum(mip_var[i][j] * comm_matrix[i][j] for i in range(shape_1) for j in range(shape_2)) 3. mem_cost += mip.xsum(mip_var[i][j] * mem_matrix[i][j] for i in range(shape_1) for j in range(shape_2)) 4. 遍历[up_out_strategy_list,down_in_strategy_list]大小的矩阵添加总cost中. 5. 再次遍历所有的cluster edge 6. 添加[up_out_strategy_list,down_in_strategy_list]的binary var矩阵和为1的约束, 这样确保只选择一种切分 7. 添加上下连接关系的约束, 也就是输入/输出选择某种切分, 那么矩阵中对应的节点也必须选择某种切分. 8. 遍历所有的cluster, 添加每个cluster只选择一个切分的约束 9. 添加目标为mip.minimize(comm_cost + 0.00000001 * mem_cost) 6. 求解并提取出新的graph

总结

以上内容都是在浏览的时候记录的, 如果有部分内容理解错误可以在评论区指出. 总的来说easydist的shard annotation部分以及combination annotation的设计的很优雅, 通过shard_id的方式把一些计算上有依赖的维度的依赖关系表示出来了, 如果是SPMD的表示方式, 需要编写代码时自己维护这种相关性. 后者可以在没有添加推导函数的情况下自动做一些切分推导, 并且可以通过偏函数的方式进行组合, 代码复用程度高.

后续的meta graph转换部分我看的比较困难, 主要是各种数据结构的交互比较多, 还有就是因为代码中有一些入侵的修改类实例的地方比较难读. 不过总体来讲就是切子图,然后添加候选集.最后就是用一个约束模型来求解.

相比起easydist, 我自己实现的自动分布式切分方法就比较暴力, 直接列出所有的可切分方式以及必要情况下的重新切分方式作为候选集, 然后结合通信/计算/内存移动开销进行求解.

全部的候选集: 求解出来的图: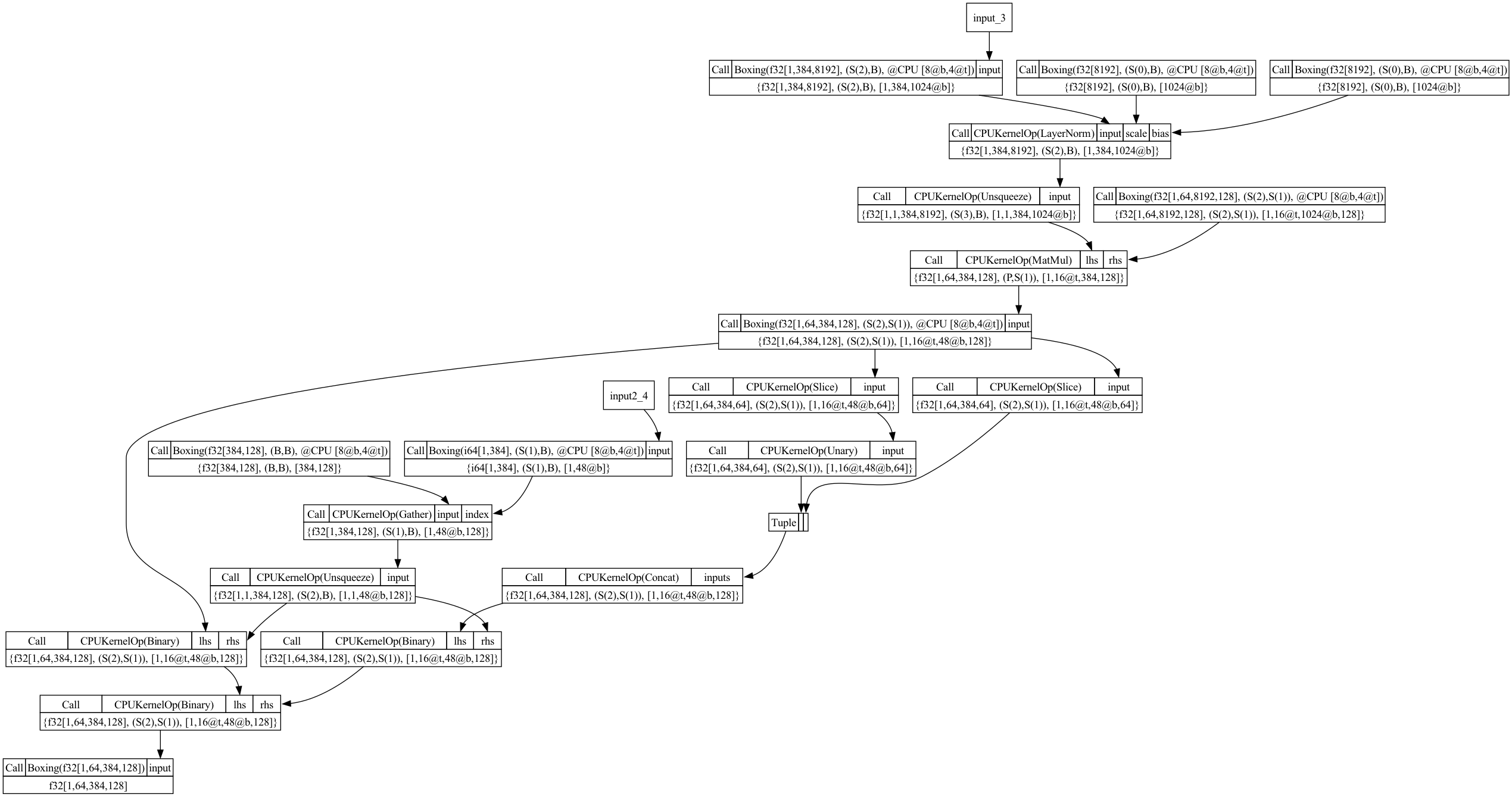

待解决的问题

虽然自动分布式切分搜索可以解决选择切分方式的问题, 但是预计还会有许多别的问题, 这里抛砖引玉提出一些, 希望可以和大家多多讨论:

1. 子图合并的问题

自动并行切分通常只考虑了通信上的开销, 没有考虑带宽瓶颈导致的性能损失以及静态内存分配的优化带来的性能提升. 比如一些带宽瓶颈的操作或者一些concat/view的操作原本可以通过编写高性能fused kernel来进行优化, 有可能自动切分会在这些算子中间添加了reshard, 那么硬件利用率就不高了. 所以可能还是需要先匹配到可以做合并的算子再做自动并行切分, 但是这个事情需要手动来做, 手动来实现还需要考虑合并那些部分, 都是比较复杂的问题.

2. 流水并行问题

流水并行没有办法在自动切分搜索的时候体现, 如果在切分搜索的时候贪心的找到前面n层可在gpu上放下的层, 但是不同的分布式切分也会影响内存使用大小, 此时只能贪心的去添加层没法做到整体最优. 或者通过手动的方式去划分出一个子图进行自动切分搜索.

3. 重计算问题

如果对resize/conv来说如果切分了h/w, 那么就需要考虑上面的层需要多计算一部分数据, 那就需要引入bounds infer了. 当然如果不考虑这样切分就不会有这个问题.