探索AMX: 解锁Apple Silicon隐藏性能
自从2020年Apple发布的芯片M1/M2/M3, 至少提供了四种不同的方式可以执行高负载的计算任务:
标准的ARMv8 SIMD/NEON向量指令集.
苹果尚未公开文档的AMX(Apple Matrix Co-processor)指令集, 由CPU发射, 在特殊的加速器上运行.
神经网络处理器ANE(Apple Neural Engine)
Metal GPU
在M1 Max上单核计算单精度浮点矩阵乘法时, 使用SIMD指令集可达到102 GFLOPS左右的性能, 而使用AMX指令集最多可达到1475 GFLOPS! 本文就来带领大家一同探索AMX指令集, 学习如何解锁这剩下的14倍算力.
1. 概述
先通过一张图建立起对于AMX初步了解. 考虑一个32x32的计算单元网格, 每个单元可以执行16位乘积, 或者2x2单元子网格可以执行32位乘积, 或者4x4子网格可以执行64位乘积. 为了提供此网格的输入, 有一个包含32个16位元素(或16个32位元素, 或8个64位元素)的X寄存器池, 以及一个同样包含32个16位元素(或16个32位元素, 或8个64位元素)的Y寄存器池. 使用单个指令可以执行完整的外积: 将X寄存器的每个元素与Y寄存器的每个元素相乘, 并在相应位置与Z元素一起累加. 或者可以将X寄存器的每个元素与Y寄存器的每个元素进行内积, 得到一个点的结果.
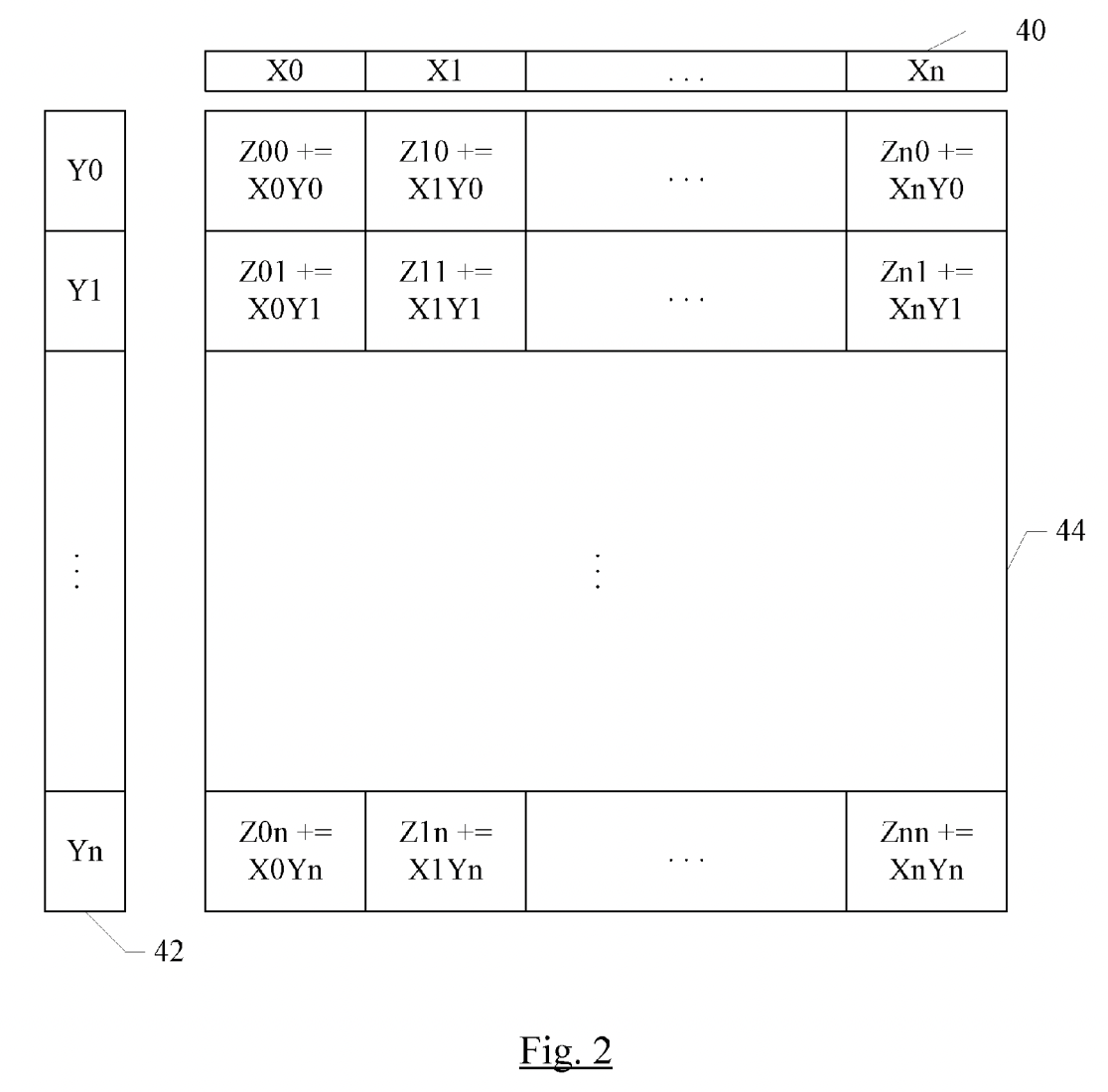
AMX为以上的操作提供了LDX/LDY, FMA, LDZ/SDZ等指令. 其中FMA分为Matrix Mode和Vector Mode分别对应外积与内积两种不同的计算方式. 当然我们首选外积, 否则无法最大化利用硬件. 下面两张图分别展示了内积与外积的计算方式:
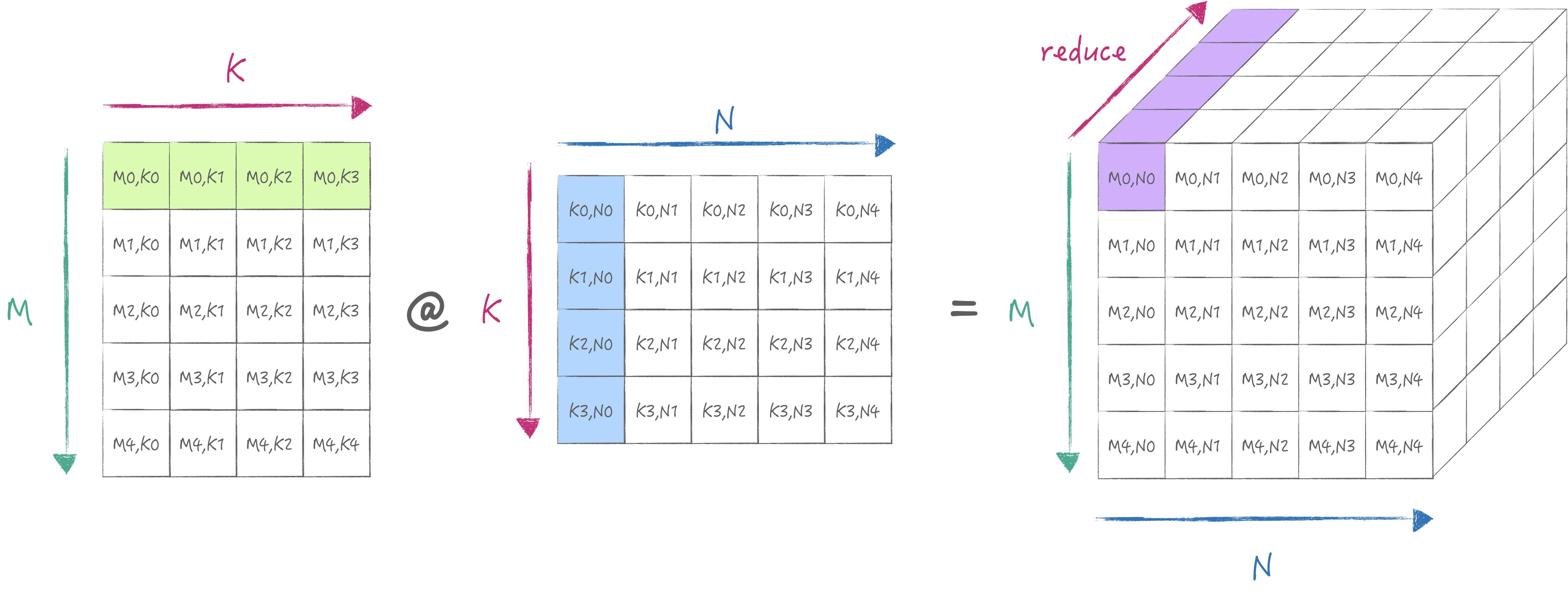
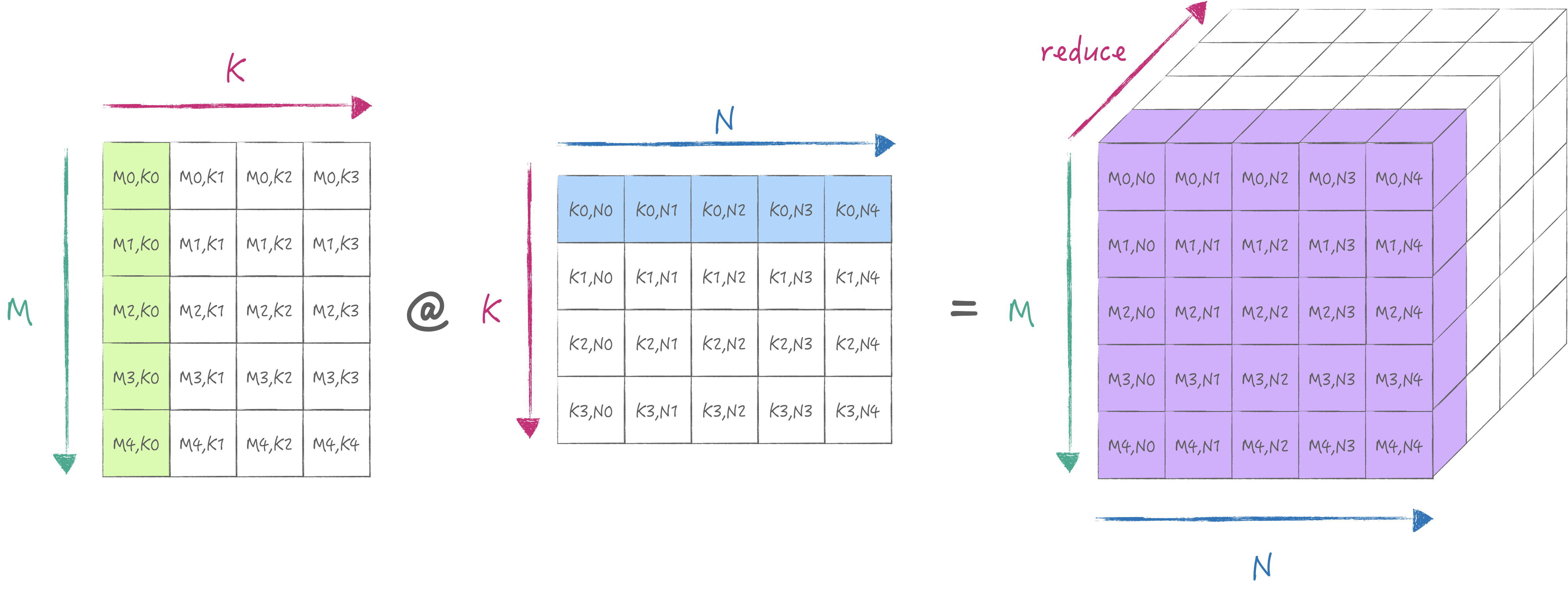
2. 最小计算流程
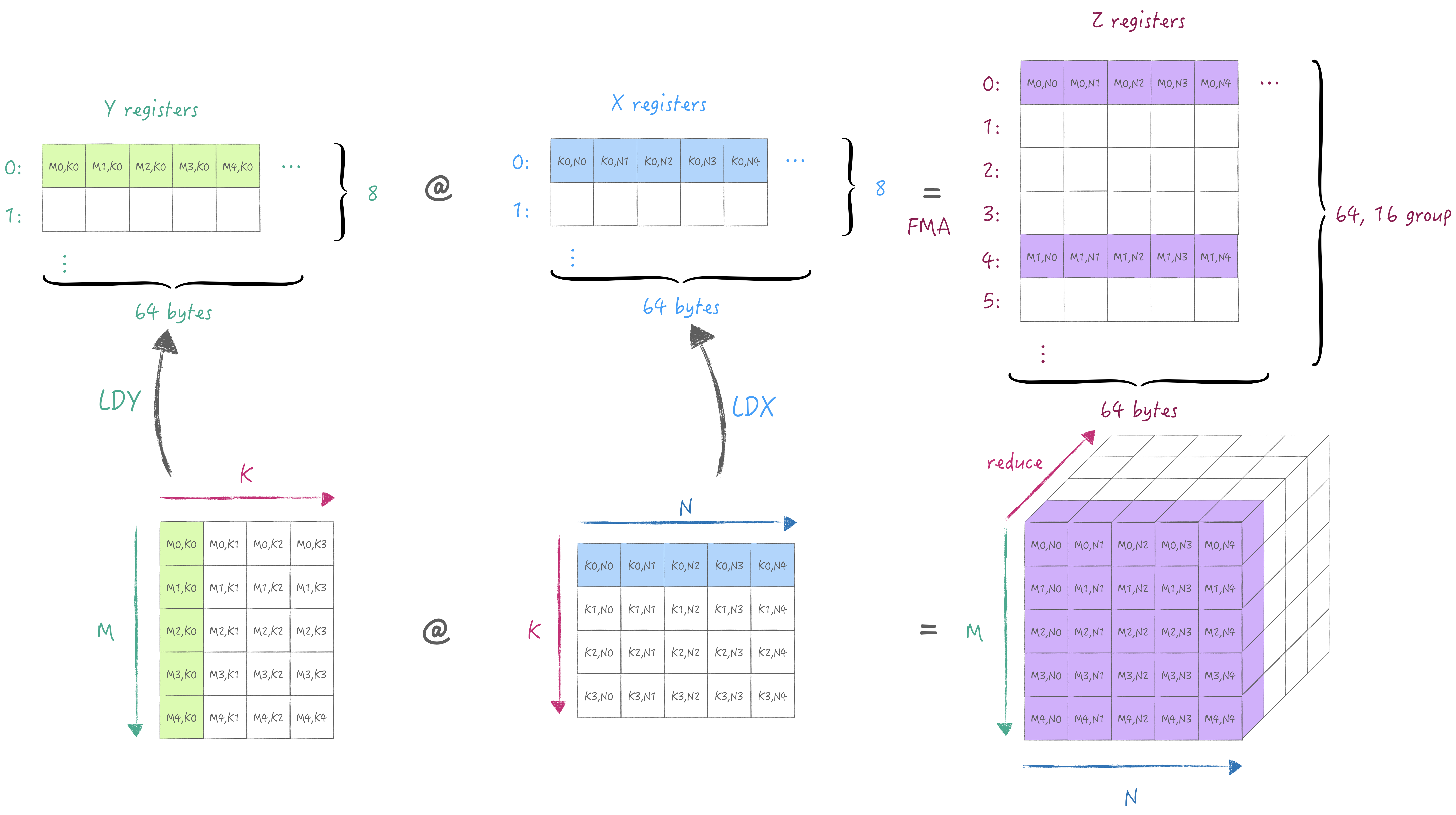
下面同样通过一张图解释清楚AMX中的寄存器规格与最小计算流程. 首先是X/Y寄存器池, 他们各有8个宽度为64 bytes的寄存器, 可以存储fp16/32/64或者i8/16/32,u8/16/32类型的数据. 接着是Z寄存器池, 他有64个宽度为64 bytes的寄存器, 用于存储X/Y寄存器外积或内积的结果. 根据第一节中描述, 2x2单元子网格来执行32位乘积, 因此执行外积时需要用到16个寄存器, 因此64个寄存器被分16组, 每组的间隔为4(64/16), 即外积结果并非是按寄存器连续存储的. (注意AMX只支持从主存中加载与存储, 无法通过通用寄存器/向量寄存器加载与存储)
通过外积计算可以获得一个partial sum存储在Z寄存器池中, 接下来我们可以切换K维度从而累积partial sum得到完整的结果:
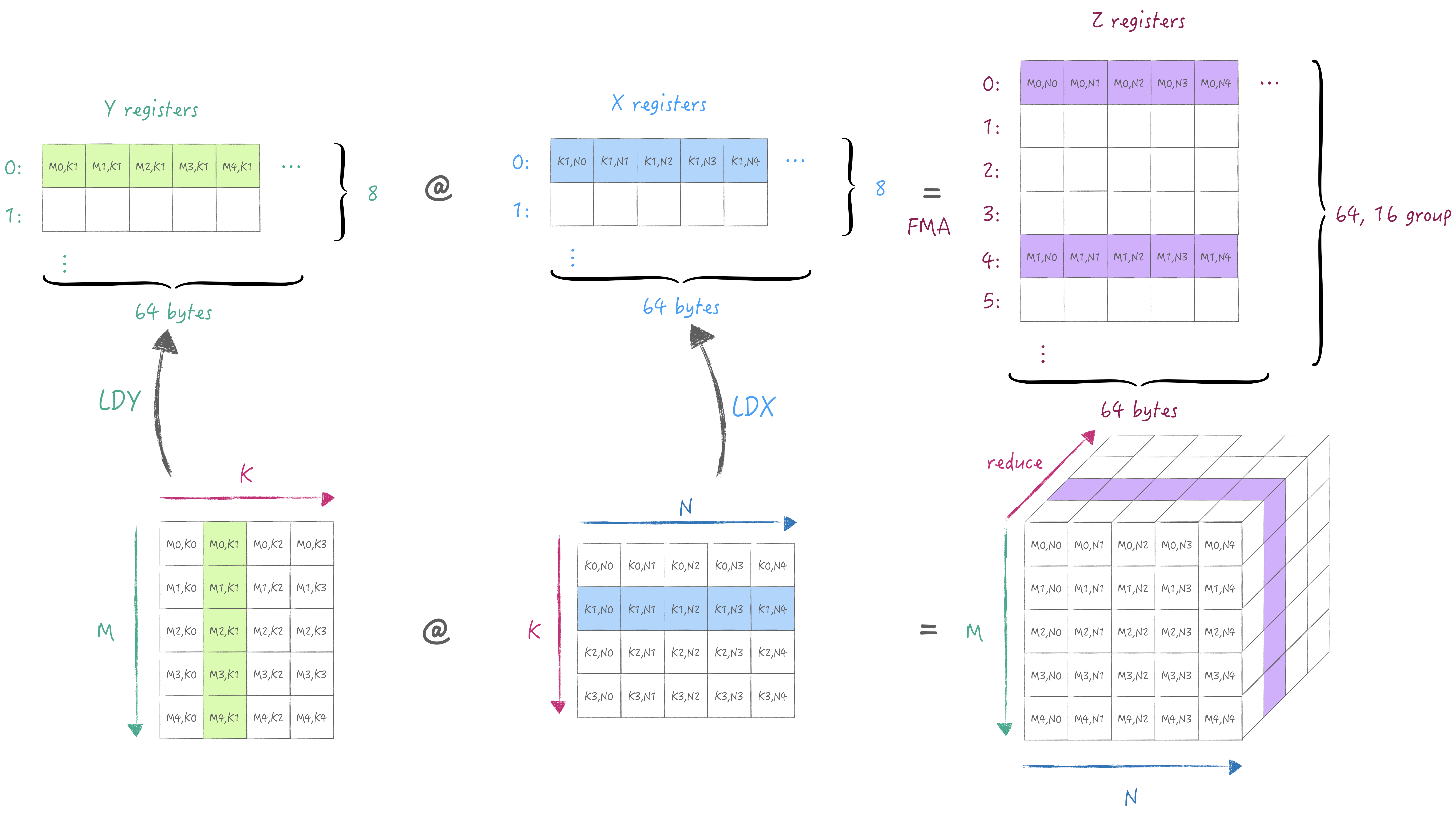
此时重新加载不同K维度的A/B矩阵, 然后将计算结果写入到与之前同一个Z的寄存器组中实现累加.
当然也可以迭代M/N, 比如这个例子中保持M不变, 迭代到下一个N,
此时我们需要在Z寄存器池中另外选一组存储当前M/N的累加值: 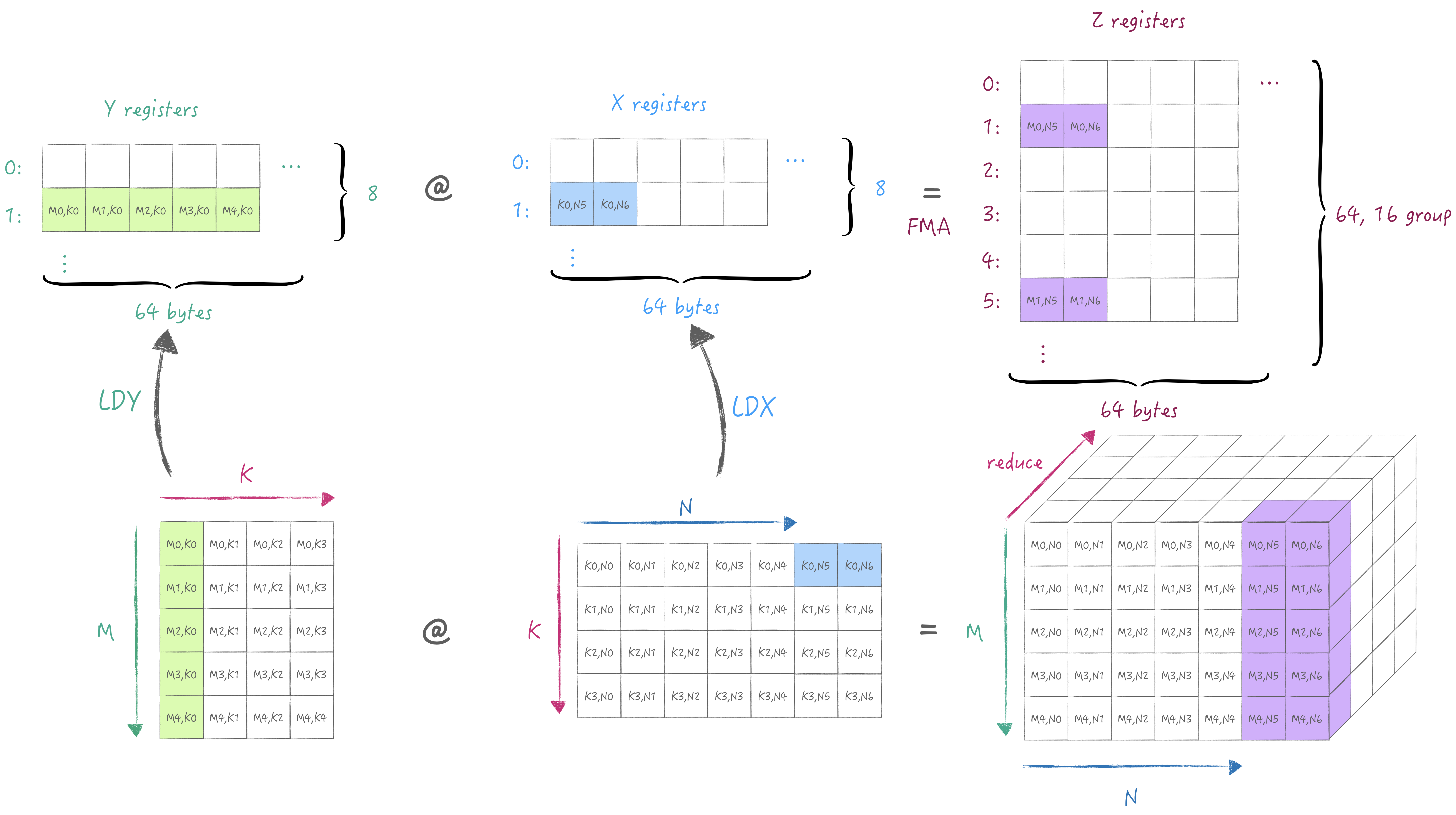
3. 理论性能测试
为了用好AMX, 首先需要更加了解AMX的相关参数, 接下来一起验证理论各项性能指标.
3.1 理论计算性能
根据上一节我们清楚了Z寄存器组在float32模式下一共被分为了16组, 一次计算在每一组中得到一列结果, 因此ALU实际上被分为了4组. 这里就来验证使用不同个数的ALU组的峰值性能:
perf_func = [&z_nums]() { |
得到结果如下:
| ALU Nums | Gflop/s |
|---|---|
| 1 | 405.530 |
| 2 | 826.912 |
| 3 | 1244.570 |
| 4 | 1666.952 |
这表明虽然每组ALU是单独配置和发射, 但是他们之间是可以并行执行的.
3.2 理论数据加载性能
这里是我设计的性能测试用例, 其中reg nums表示X/Y寄存器池.
near表示是否读取内存中连续的地址,在M2 Pro中l1 Dcache
大小为65536, 因此将K设计为数倍大于l1 cache size,
当near == 0时需要跨过两倍大小的cache size去读取.
width表示一次读取几个寄存器个数, 最大为4.
constexpr size_t K = (65536 / 4 / (16 * 4)) * 4; |
接下来我们计算数据加载时间, 得到下表:
| Reg Nums | Near | X Width | Y Width | GB/s |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 87.1489 |
| 1 | 1 | 2 | 0 | 213.164 |
| 1 | 1 | 4 | 0 | 456.332 |
| 1 | 0 | 1 | 0 | 120.796 |
| 1 | 0 | 2 | 0 | 260.115 |
| 1 | 0 | 4 | 0 | 483.285 |
| 2 | 1 | 1 | 1 | 134.33 |
| 2 | 1 | 1 | 2 | 162.084 |
| 2 | 1 | 1 | 4 | 297.15 |
| 2 | 1 | 2 | 1 | 201.658 |
| 2 | 1 | 2 | 2 | 214.772 |
| 2 | 1 | 2 | 4 | 350.554 |
| 2 | 1 | 4 | 1 | 384.614 |
| 2 | 1 | 4 | 2 | 349.528 |
| 2 | 1 | 4 | 4 | 476.722 |
| 2 | 0 | 1 | 1 | 130.604 |
| 2 | 0 | 1 | 2 | 163.91 |
| 2 | 0 | 1 | 4 | 254.922 |
| 2 | 0 | 2 | 1 | 195.612 |
| 2 | 0 | 2 | 2 | 213.61 |
| 2 | 0 | 2 | 4 | 298.603 |
| 2 | 0 | 4 | 1 | 310.308 |
| 2 | 0 | 4 | 2 | 302.767 |
| 2 | 0 | 4 | 4 | 325.193 |
可以发现加大读取宽度是可以翻倍带宽的, 因此这是无成本的. 读取连续摆放的数据相比于非连续读取略有提升, 这表明需要对数据摆放进行优化. 同时加载两个寄存器中也同样不会导致带宽降低, 表明可以同时加载A/B矩阵, 但需要注意尽量cache起来.
3.3 理论数据存储性能
同样在store时设计了reg_num,near,width等选项,
值的注意的是, 因为Z寄存器池被分为了16组,
所以每一次store时都将16组全部输出: constexpr size_t K = (65536 / 4 / (16 * 4)) * 2;
float CNear[16][16 * 4]{};
float C[16][K]{};
perf_func = [&C, &CNear, &near, &z_num, &width]() {
auto ldst = width == 2 ? ldstz().multiple() : ldstz();
for (size_t z = 0; z < z_num; z++) {
for (size_t m = 0; m < 16; m++) {
AMX_STZ(ldst.row_index(m * 4 + z * width)
.bind(near ? CNear[m] + 16 * z * width
: C[m] + 16 * z * width));
}
}
};
测试结果如下:
| Reg Nums | Near | Width | GB/s |
|---|---|---|---|
| 1 | 1 | 1 | 10.3769 |
| 1 | 1 | 2 | 8.93052 |
| 1 | 0 | 1 | 12.9423 |
| 1 | 0 | 2 | 12.3377 |
| 2 | 1 | 1 | 5.69731 |
| 2 | 1 | 2 | 12.3658 |
| 2 | 0 | 1 | 7.55092 |
| 2 | 0 | 2 | 13.0133 |
| 3 | 1 | 1 | 6.58085 |
| 3 | 0 | 1 | 11.4118 |
| 4 | 1 | 1 | 8.8847 |
| 4 | 0 | 1 | 9.85956 |
可以发现使用多个寄存器并无法提升带宽, 说明基本上是串行输出, 但开启两倍宽度还是可以有效提升带宽. 然而整体速度相比于计算和加载慢了数倍, 这表明我们不能频繁地加载与存储Z.
3. 设计Micro Kernel
基于上一节中的内容, 我们可以来尝试编写一个现实世界的矩阵乘法, 为了矩阵乘法的高效, 采用自底向上的准则来设计它. 也就是说, 首先需要设计一个充分利用硬件算力的micro kernel, 接着再通过合理调用micro kernel达到极限算力.
首先回顾一下最基础的计算流程, 加载一列M, 加载一行N, 计算得到一块MxN. 此时明显可以发现对于X/Y/Z寄存器池都是没用充分利用的, 特别是Z寄存器池, 这意味着只使用了\(\frac{1}{4}\)的算力, 所以首要目标是用满它.
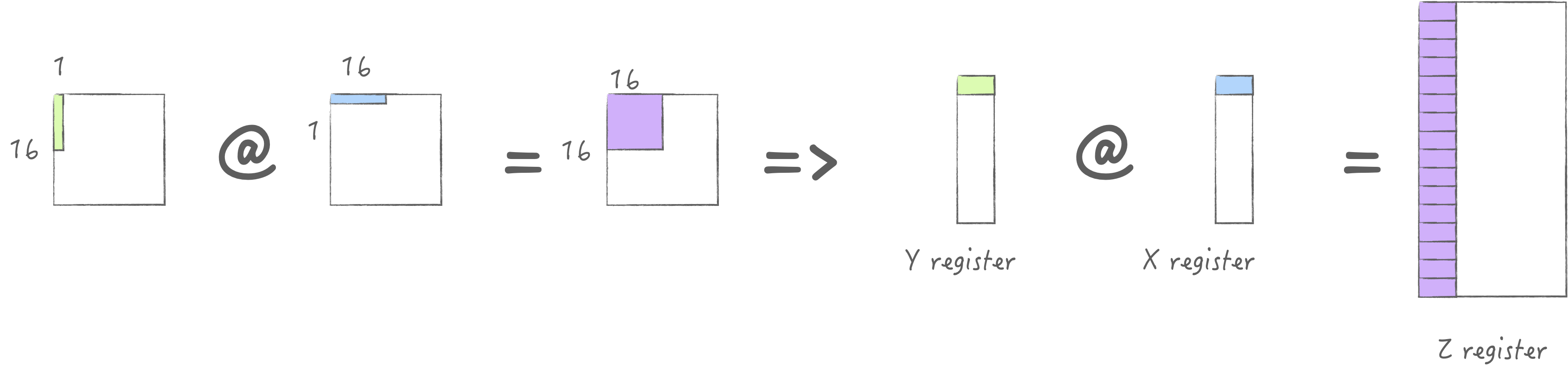
根据上一节, 我们可以已知最大理论计算性能以及带宽, 那么根据公式我们可以计算用满ALU时一次计算需要花费多少纳秒: \[ \begin{aligned} Compute Time &= \frac{FLOPs}{GFLOPS}\ ~NanoSeconds\\ Load Time &= \frac{Bytes}{GBS}\ ~NanoSeconds \end{aligned} \]
接下来我们基于这个数据来设计不同的计算策略:
3.1 计算策略1: 加载多组N
在我的M2 Pro中, AMX最大一次可以加载4*64 bytes,
因此可以加载1组M以及4组的N, 利用满计算单元得到M*4N,
然后在下一次循环中切换不同的K. 总的来说是加载一次, 计算四次,
由于X寄存器池大小限制只能多缓存一次. 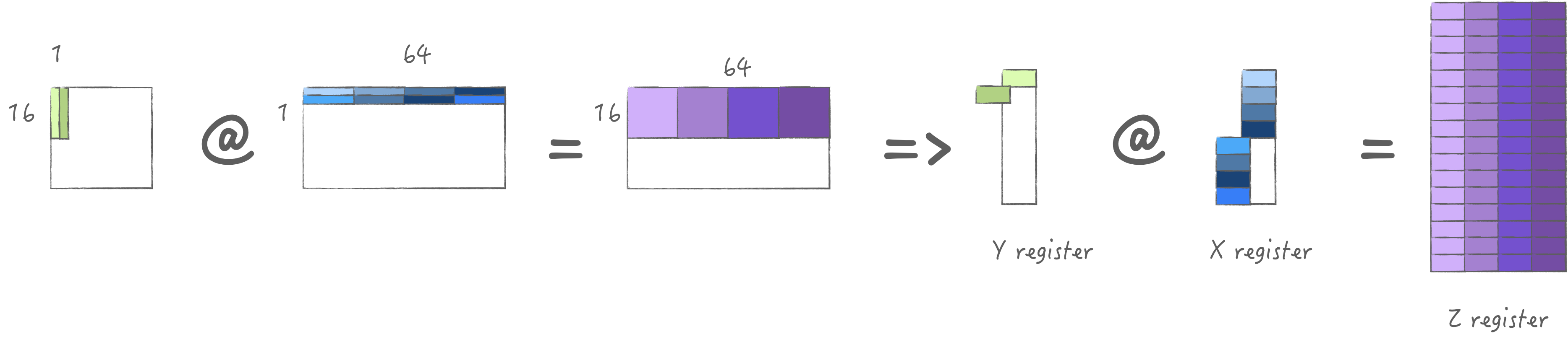
查表可知,加载带宽为254.922 GB/s,得到计算时间与数据加载时间分别为: \[ \begin{aligned} FLOPs &= 2 * M * N * 4 = 2048 \\ Compute Time &= FLOPs / 1666 = 1.229~NanoSeconds \\ Bytes &= (1 * M + 4 * N) * 4 \\ Load Time &= Bytes / 297.15 = 1.076~NanoSeconds \end{aligned} \]
两者时间基本差不多, 但他们之间的差只有0.15ns,
这点时间不足以在一次缓存中流水起来.
3.2 计算策略2: 加载多组M
同上一种策略类似, 同样也是加载一次计算四次,
计算时间与加载时间和上一小节类似,
但是这里存在一个额外问题则是对于A矩阵的列方向是不连续的,
需要先通过CPU进行转置4倍的M后才可以加载, 因此不考虑. 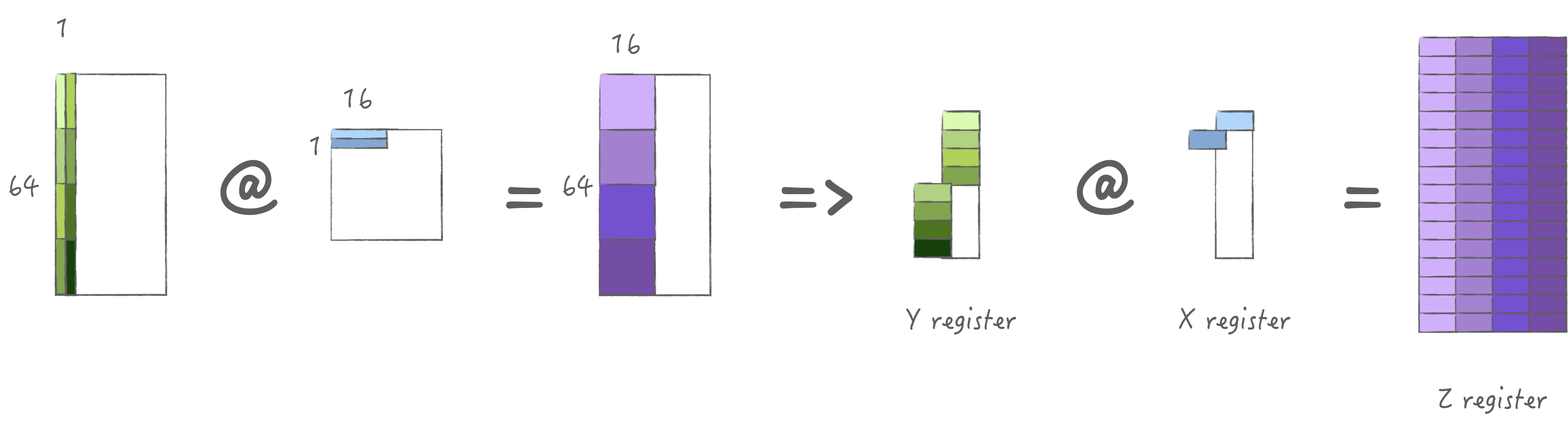
3.3 计算策略3: 加载两组M/N
为了均匀X/Y寄存器的存储, 可以考虑加载同样大小的M/N, 也就是加载2组,
此时可以计算4次得到2M*2N大小的输出,
考虑到最大可以加载4*64 bytes, 那么可以加载不同K两组M/N,
这样一次加载实际可以计算8次, 最大限度的利用算力.
此时对于X/Y寄存器池使用量是一样的, 也就是他们还可以多缓存一次: 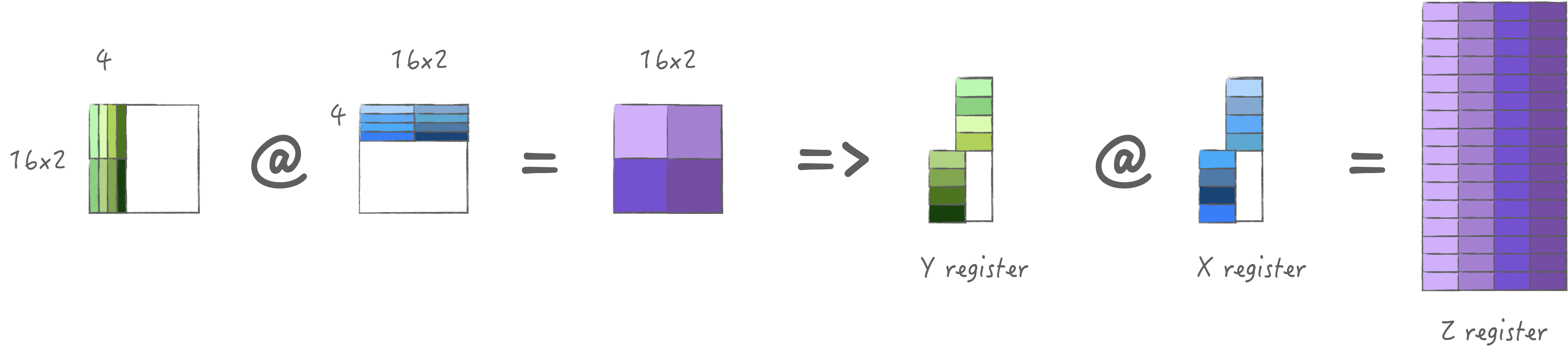
来动手计算一下,加载带宽为254.922 GB/s,得到计算时间与数据加载时间分别为: \[ \begin{aligned} FLOPs &= 2 * M * N * 4 * 2 = 4096 \\ Compute Time &= FLOPs / 1666 = 2.458~NanoSeconds \\ Bytes &= (4 * M + 4 * N) * 4 \\ Load Time &= Bytes / 476.722 = 1.074~NanoSeconds \end{aligned} \]
此时计算时间减去数据加载时间为1.384 ns,
大于下一次的计算时间1.074 ns,
那么也就表明我们可以在下一次缓存中完美的流水起来,
从而发挥出极限算力.
3.4 验证计算策略3
为了达到峰值的数据加载性能, 我们需要对矩阵进行布局优化,
也就是将A/B矩阵分别以32为宽度进行pack, 这样加载时是满足内存连续读取,
同时一次可以计算得到2*M*N的结果, 其具体迭代流程图如下: 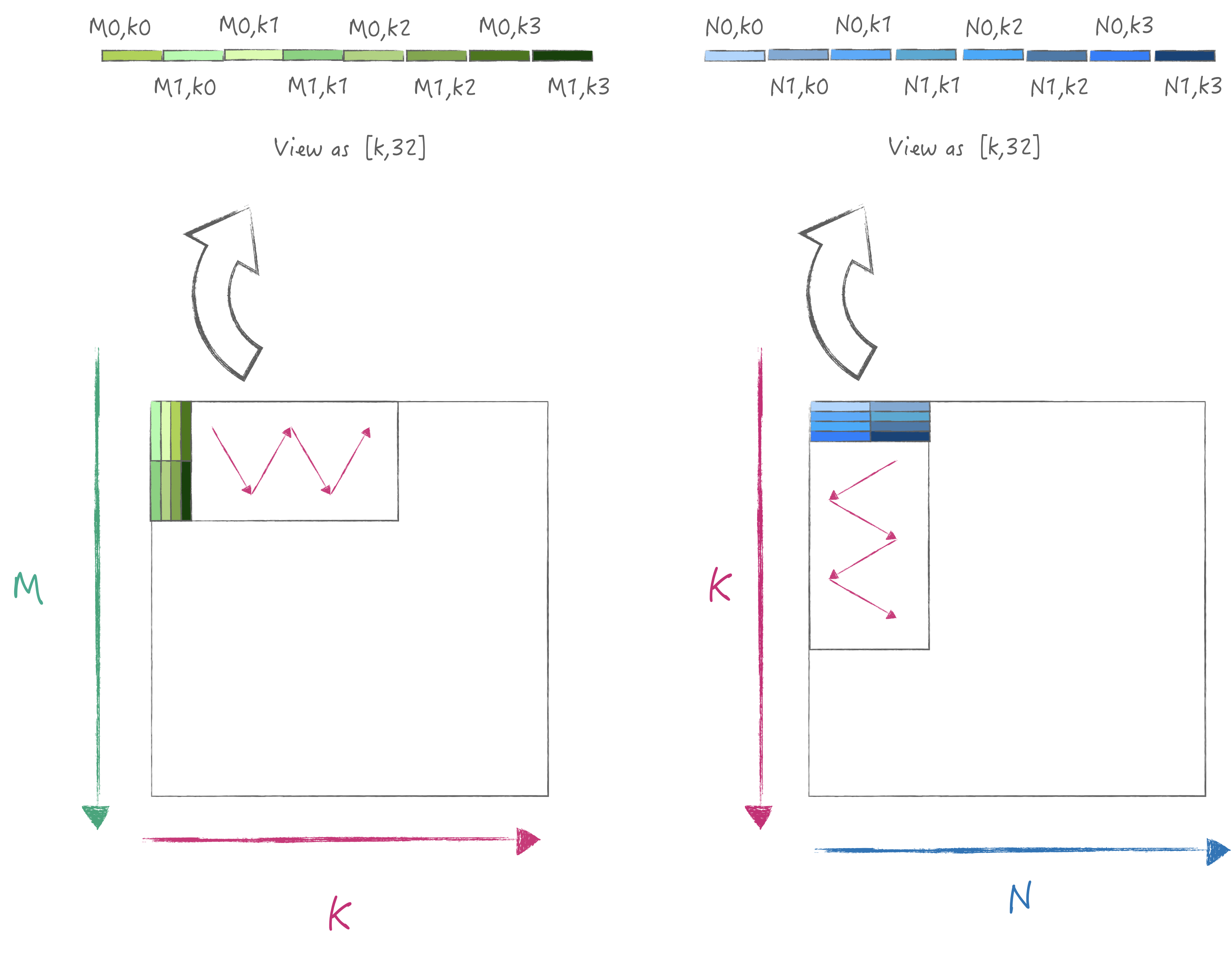
为了简单起见我假设M/K/N都满足最小计算单元的倍数,
同时要求输入A/B矩阵都是经过布局优化的, 下面则是具体的代码:
template <bool LoadC, bool StoreC, size_t KTile, size_t M, size_t N>
void gepdot(size_t curM, size_t curK, size_t curN,
const float packedA[KTile][32], const float packedB[KTile][32],
float C[M][N]) {
static_assert(KTile % 4 == 0, "not support k%4!=0");
if constexpr (LoadC) {
// load acc value.
for (size_t om = 0; om < 2; om++) {
for (size_t m = 0; m < 16; m++) {
AMX_STZ(
ldstz().row_index(m * 4 + om * 2).multiple().bind(C[om * 16 + m]));
}
}
}
for (size_t k = curK; k < curK + KTile; k += 4) {
for (size_t ok = k; ok < k + 4; ok += 2) {
// load [m0,k0], [m1,k0], [m0,k1], [m1,k1]
AMX_LDY(ldxy().register_index(0).multiple().multiple_four().bind(
(void *)packedA[ok]));
// load [n0,k0], [n1,k0], [n0,k1], [n1,k1]
AMX_LDX(ldxy().register_index(0).multiple().multiple_four().bind(
(void *)packedB[ok]));
// compute 8 times.
// [[m0,n0],[m0,n1],
// [m1,n0],[m1,n1]]
for (size_t ik = ok; ik < ok + 2; ik++) {
auto fma = ik == 0 ? fma32().skip_z() : fma32();
for (size_t m = 0; m < 2; m++) {
for (size_t n = 0; n < 2; n++) {
AMX_FMA32(fma.z_row(m * 2 + n)
.y_offset((ik - ok) * 2 * 16 * 4 + m * 16 * 4)
.x_offset((ik - ok) * 2 * 16 * 4 + n * 16 * 4));
}
}
}
}
}
// last time need store C.
if constexpr (StoreC) {
for (size_t om = 0; om < 2; om++) {
for (size_t m = 0; m < 16; m++) {
AMX_STZ(
ldstz().row_index(m * 4 + om * 2).multiple().bind(C[om * 16 + m]));
}
}
}
}
在M = 16 * 2, K = 8192, N = 16 * 2的情况下测试,
得到1632.13 Gflop/s的性能,
达到了峰值性能的0.979%.: [----------] 1 test from test_amx
[ RUN ] test_amx.test_gepdot
Gflop/s: 1632.13
[ OK ] test_amx.test_gepdot (1032 ms)
[----------] 1 test from test_amx (1032 ms total)
4. 设计分块方案
如果在没有AI Compiler提前优化的情况下, 我们是没办法得到内存优化好的输入数据的, 那么就需要考虑计算的同时进行布局优化. 并且上一节的例子中我没有设置很大的M和N, 而现实中需要切换M与N, 此时又带来另一个分块大小的问题.
如果是使用SIMD来进行计算, 那么论文Anatomy of High-Performance Matrix Multiplication中已经给出了一个很好的分块解决方案:
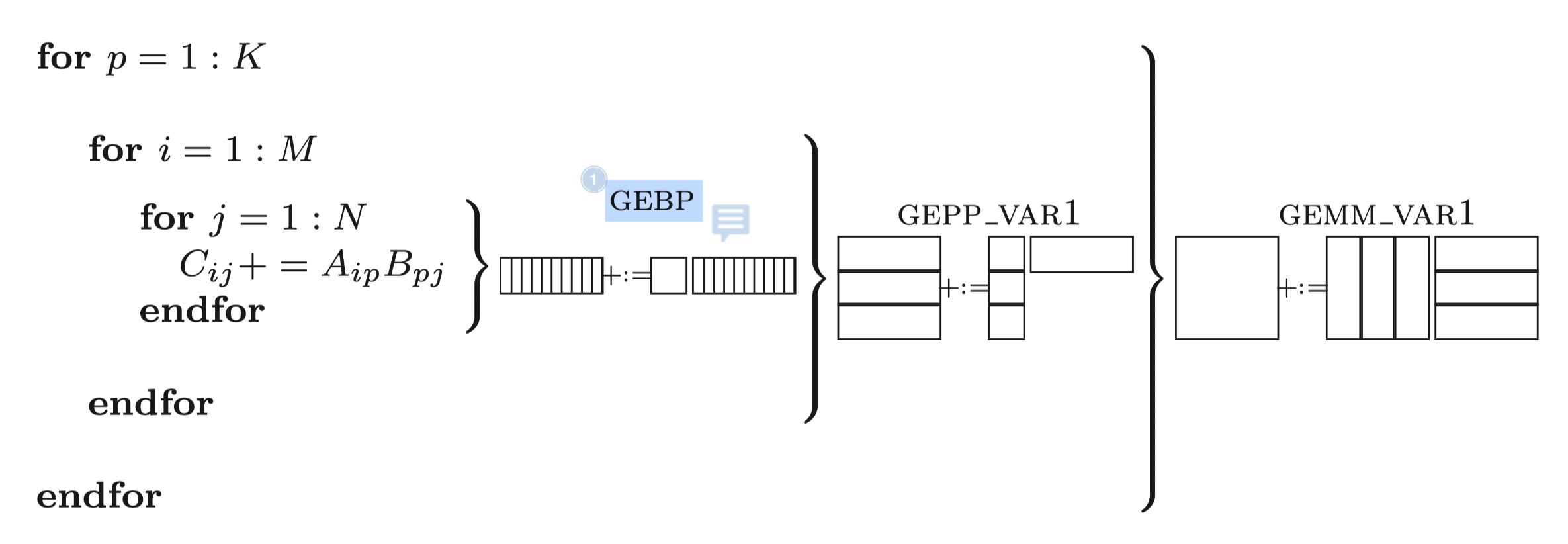
即最内层使用gebp核.
但是gebp它需要反复的加载和存储C矩阵,
对于CPU寄存器来说他的带宽足够大,
只需要Nr远大于Kc就可以均摊掉访问C矩阵的内存开销,
对于AMX来说Z寄存器的带宽只有X/Y寄存器带宽的几十分之一, 显然是无法均摊的,
因此我们肯定不能采用论文中的计算方法: 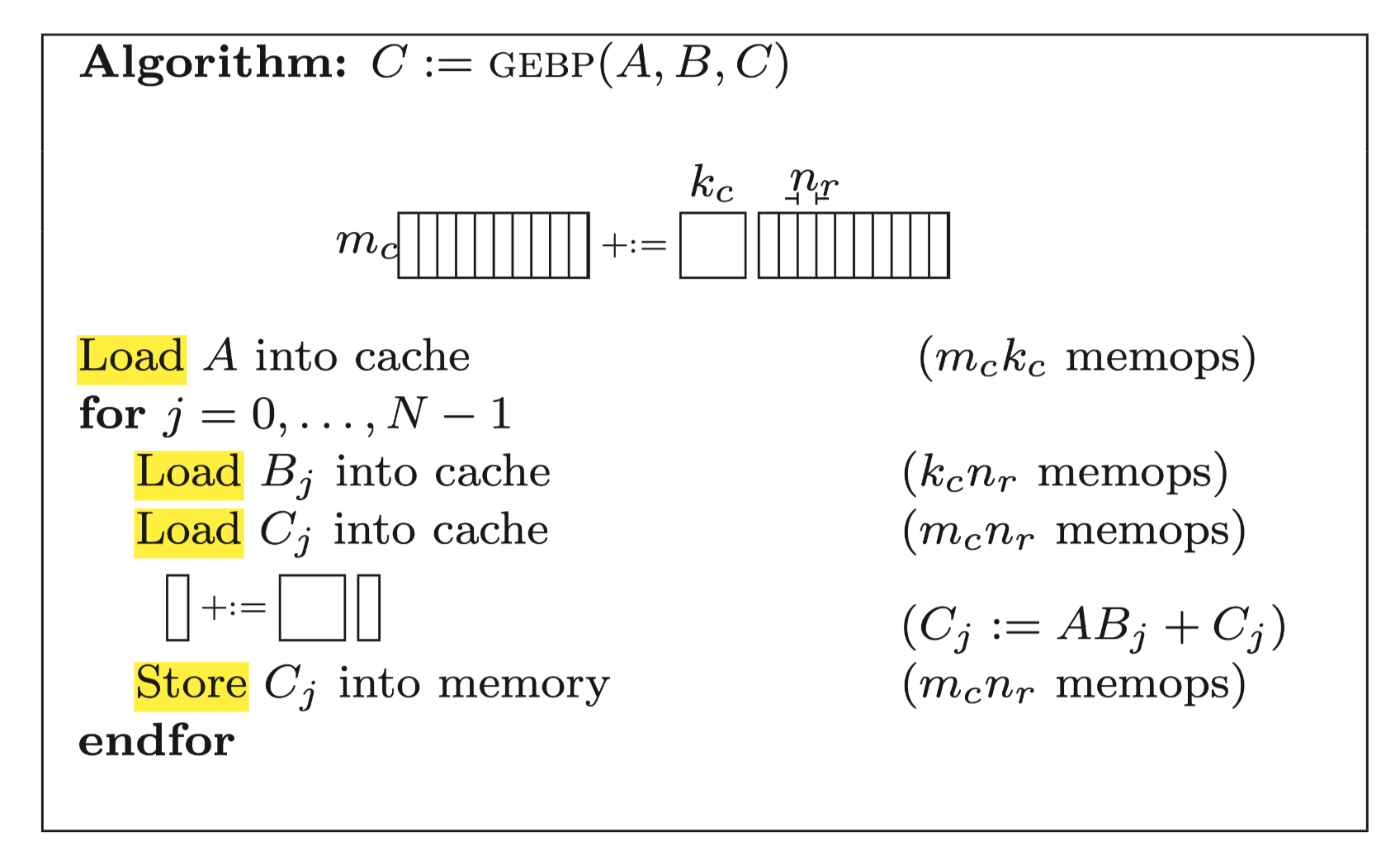
因此我这里抛砖引玉, 实现了一个简易的两级分块策略,
M中循环N用于复用A矩阵, 把K迭代放在循环最内层以适配gepdot核,
同时在每个KTile中pack一小块A并缓存起来, 这样循环N时可以避免重复执行:
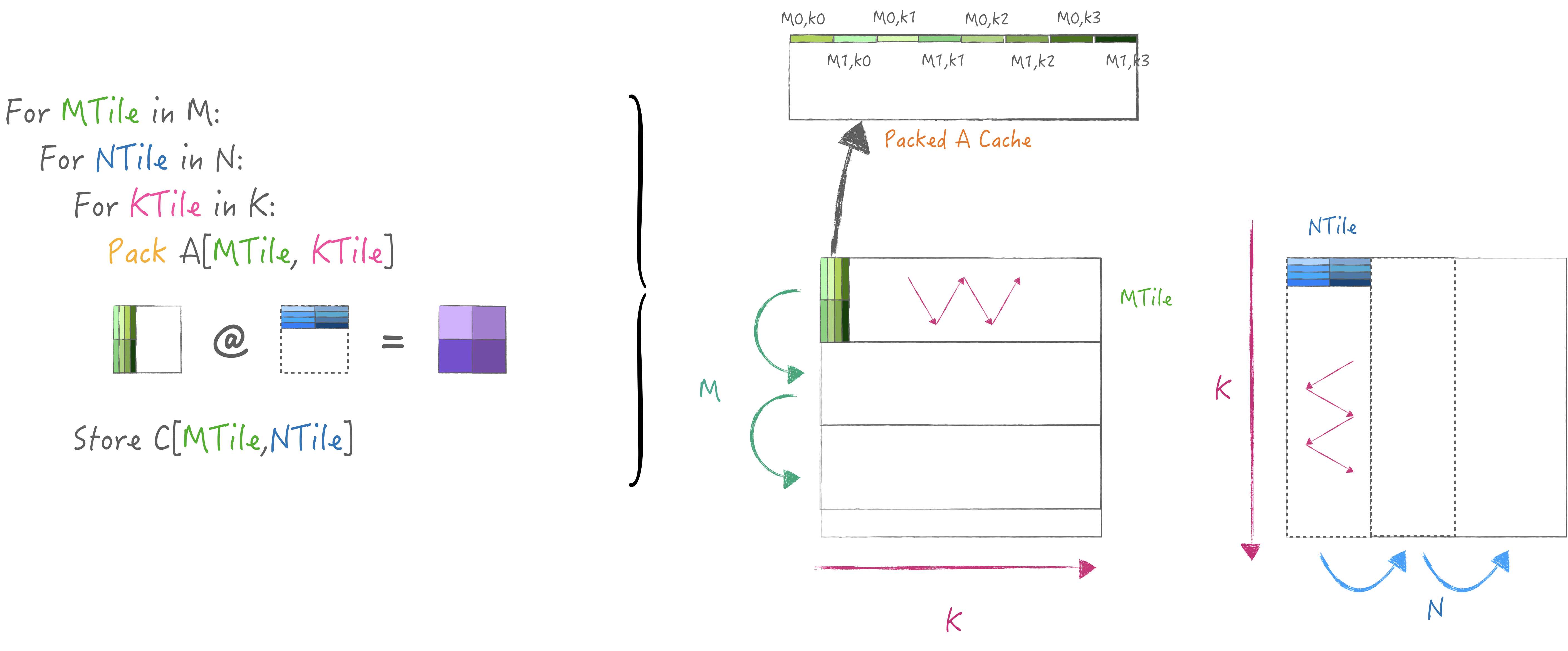
最终代码如下: auto matmul = [&]() -> void {
constexpr size_t KTile = 32, MTile = 32, NTile = 32;
for (size_t mo = 0; mo < M; mo += MTile) {
float PackedA[K][MTile];
for (size_t no = 0; no < N; no += NTile) {
for (size_t ko = 0; ko < K; ko += KTile) {
// each time pack local innertile.
if (no == 0) {
for (size_t mi = 0; mi < MTile; mi++) {
for (size_t i = ko; i < ko + KTile; i++) {
PackedA[i][mi] = A[mo + mi][i];
}
}
}
gepdot_general<KTile, M, K, N>(false, (ko + KTile == K), mo, ko, no,
PackedA + ko, B, C);
}
}
}
};
测试性能达到了Apple所提供库的70%性能:
[ RUN ] test_amx.test_gepdot_general |
其实计算策略3中是计算瓶颈的,
按理论值计算流水之后实际大约还剩0.3ns时间可以分配给数据加载,
如果可以很好的建模CPU内存操作耗时, 理论上是可以做到把pack
A矩阵的过程掩盖起来, 从而达到理论峰值. 不过从cblas_sgemm的实测性能来看,
应该也没有完全掩藏起来,
超越Apple闭源库这个具有挑战性的任务就交给读者们了👻.
5. 疑问
我设计了一个测试AMX加载数据是否会更新cache的用例: constexpr size_t K = (65536 / 4 / (16 * 2)) * 8; /* 65536 是cache size */
float N[1][16 * 2]{};
float M[K][16 * 2]{};
float *C = (float *)malloc(K * 65536);
auto func1 = [&N]() {
for (size_t i = 0; i < K; i++) {
AMX_LDX(ldxy().multiple().register_index(0).bind((void *)N[0]));
}
}
auto func2 = [&M]() {
for (size_t i = 0; i < K; i++) {
AMX_LDX(ldxy().multiple().register_index(0).bind((void *)M[i]));
}
}
auto func3 = [&C]() {
for (size_t i = 0; i < K; i++) {
AMX_LDX(
ldxy().multiple().register_index(0).bind((void *)(C + i * K)));
}
}
其中func1永远只加载同一个位置的数据, func2按顺序加载连续的数据,
func3每次加载跨度大于l1 cache size的数据, 最终结果如下:
func1: 29.9743 GB/s
func2: 219.201 GB/s
func3: 9.74711 GB/s
func2与func3的结果表示l1 cache对于AMX来说也是重要的, 但是我无法理解func1与func2的差异, 理论上被访问过的数据应该会缓存在cache中, 而从结果上来看被缓存的似乎是当前所加载地址后面部分的数据, 这个问题可能需要更了解体系结构的读者才能解答.
6. 总结
至此本文所有的内容介绍完毕, 我所使用的全部测试代码在这里获取(Verified on M2 Pro). 而本文所依赖的信息来源于Peter Cawley等人的逆向成果, 其中包含了更多指令介绍以及使用方法.