这是zheng size的一篇分析建模的文章,思路和Model
Driven Optimization 类似,但是细节上有一些差异,简单总结一下。
Block Decomposition
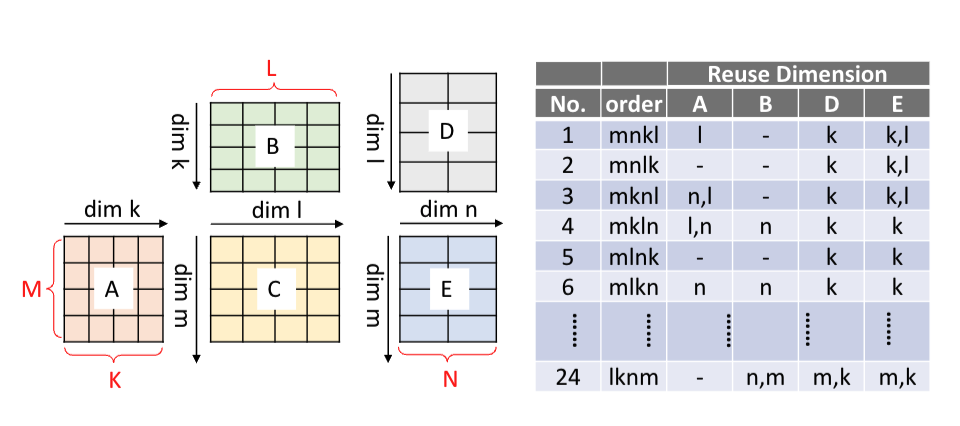
首先给定一个两个矩阵乘的例子, 下图中隐含了他的reuse
dim的计算方式:
reuse_dims = perms[last_access_dim(buffer, perms) + 1 :]
比如上图中mnkl的顺序,其中m,k参与访问A,
因此只有l是reuse dim.
分层是为了单独求解当前层的循环顺序,因为在Model Driven Optimization中说了,如果两个层级,那么他们的循环并不是全部组合,而是分层组合。
然后每个层在给定的loop
order中计算DV,MU,这里的Decomposition parameters S就是tile
var。计算DM的逻辑比Model Driven Optimization进行了一些简化,如果是reuse
dim就跳过,否则就乘上。
我理解他是认为他后面已经限制了sum(MU) < capacity,所以不存在超过cachesize的问题了。
input : Operator chain Opsinput : Permutation Perm = (lp1, lp2, ..., lpI )input : Decomposition parameters S = (s1, s2, ..., sI)output : data movement volume DV output : memory usage MU DV = 0 , MU = 0 for op in Ops: total_DF = 0 for tensor T in op.allTensors(): DF = getFootprint(T, S) total_DF += DF if T in Ops.IOTensors(): DM = DF keep_reuse = true for loop lpi in reversed (Perm): if lpi in op.allLoops(): if lpi accesses tensor T: keep_reuse = false if not keep_reuse: DM *= ceil(Lpi / spi) DV += DM for loop lpi in Perm: if lpi is private to op: Perm.erase(lpi) MU = max (MU, total_DF) return DV, MU
通过这个算法计算之后,在mlkn的顺序下得到:
DM
\(MK \frac{L}{T_L}\) \(KL \frac{M}{T_M}\) 0
$ NL $
MN \(\frac{L}{T_L}\)
DF
\(T_MT_K\) \(T_KT_L\) \(T_MT_L\) \(T_LT_N\) \(T_M T_N\)
所有访问到的数据都存在cache中,所以DF是通过access
dim的tile来计算,DM这里是全部的access
dim乘非reuse的次数。但是我还是有点疑惑,如果数据都在cache中,以MLK的顺序访问A真的会有重复load吗。
然后在约束MU的情况下最小化DV, \[
\begin{aligned}
DV_{GEMM\ Chain} &=D M_{A}+D M_{B}+D M_{C}+D M_{D}+D M_{E} \\
& = M K\left\lceil\frac{L}{T_{L}}\right\rceil+K
L\left\lceil\frac{M}{T_{M}}\right\rceil+N
L\left\lceil\frac{M}{T_{M}}\right\rceil+M
N\left\lceil\frac{L}{T_{L}}\right\rceil \\
MU &=max \left\{GEMM 1_{M U}, GEMM 2_{M U}\right\} \\
GEMM1_{M U} &=D F_{A}+D F_{B}+D F_{C}=T_{M} T_{K}+T_{K} T_{L}+T_{M}
T_{L} \\
GEMM 2_{M U} &=D F_{C}+D F_{D}+D F_{E}=T_{M} T_{L}+T_{L} T_{N}+T_{M}
T_{N} \\
min_{\vec{S}}\ DV_{GEMM\ Chain},\ &s.t. MU \leq MemoryCapacity (1)
\end{aligned}
\]
Optimization for
Multi-level Memory Hierarchy
对于多内存层级,他的思路与Model Driven Optimization一致,也是假设数据移动可以并行,最小化最大的数据移动cost。
\[
\begin{gathered} min _{\vec{S_{1}}, \vec{S_{2}}, ...,
\vec{S_{D}}}\left\{max \left\{Cost_{1}\left(\vec{S_{1}}\right), ...,
Cost_{D}\left(\vec{S_{D}}\right)\right\}\right\}, \\ s.t. MU_{1} \leq M
C_{1}, ..., MU_{D} \leq M C_{D} \end{gathered}
\]
Implementation
我尝试对这篇论文做了一下复现, 最后的结果如下,
但感觉搜索到的k还是比较小,循环顺序还是比较合理的,倾向于把k移动到最内层:
best perm: ('m', 'n', 'k'), ('m', 'n', 'k') best tile: ( 1 , 1, 512), ( 4, 4, 1), (m:64, k:4, n:16), 180866
import itertoolsfrom amplpy import AMPLdef solve_with_perms (all_perms: list [list [str ]] ): ap = AMPL() ap.eval ('reset;' ) ap.eval (""" var L2_m integer; var L2_k integer; var L2_n integer; var L1_m integer; var L1_k integer; var L1_n integer; var L0_m integer; var L0_k integer; var L0_n integer; var L2_A_DF = (L1_m * L0_m) * (L1_k * L0_k) * 4; var L2_B_DF = (L1_n * L0_n) * (L1_k * L0_k) * 4 * 4 * 4; var L2_C_DF = (L1_m * L0_m) * (L1_n * L0_n) * 4 * 4 * 4; var L1_A_DF = (L0_m) * (L0_k) * 4; var L1_B_DF = (L0_n) * (L0_k) * 4 * 4 * 4; var L1_C_DF = (L0_m) * (L0_n) * 4 * 4 * 4; """ ) access = { 'A' : ['m' , 'k' ], 'B' : ['n' , 'k' ], 'C' : ['m' , 'n' ] } for level in [2 , 1 ]: for bf in ['A' , 'B' , 'C' ]: level_perms = all_perms[len (all_perms) - level] params = [f'L{level} _{bf} _DF' ] axis = len (level_perms) - 1 while axis >= 0 and level_perms[axis] not in access[bf]: axis -= 1 while axis >= 0 : params.append(f'L{level} _{level_perms[axis]} ' ) axis -= 1 dm = f'var L{level} _{bf} _DM = {" * " .join(params)} ;' ap.eval (dm) ap.eval (""" subject to L2_m_c: L2_m >= 1; subject to L2_k_c: L2_k >= 1; subject to L2_n_c: L2_n >= 1; subject to L1_m_c: L1_m >= 1; subject to L1_k_c: L1_k >= 1; subject to L1_n_c: L1_n >= 1; subject to L0_m_c: L0_m >= 1; subject to L0_k_c: L0_k >= 1; subject to L0_n_c: L0_n >= 1; subject to M_c: (L0_m*L1_m*L2_m) = 256; subject to K_c: (L0_k*L1_k*L2_k) = 2048; subject to N_c: (L0_n*L1_n*L2_n) = 64; var l1_DF = (L1_A_DF + L1_B_DF + L1_C_DF); var l2_DF = (L2_A_DF + L2_B_DF + L2_C_DF); subject to l1_capacity_c: l1_DF <= (512 * 1024); subject to l2_capacity_c: l2_DF <= (1024 * 1024); """ ) ap.eval (""" var mem_cost integer; subject to max_c2: ((L2_A_DM + L2_B_DM + L2_C_DM) / 64) <= mem_cost; subject to max_c1: ((L1_A_DM + L1_B_DM + L1_C_DM) / 16) <= mem_cost; minimize total_cost: mem_cost; """ ) ap.solve(solver='couenne' ) L2_m = ap.get_value('L2_m' ) L2_k = ap.get_value('L2_k' ) L2_n = ap.get_value('L2_n' ) L1_m = ap.get_value('L1_m' ) L1_k = ap.get_value('L1_k' ) L1_n = ap.get_value('L1_n' ) L0_m = ap.get_value('L0_m' ) L0_k = ap.get_value('L0_k' ) L0_n = ap.get_value('L0_n' ) total_cost = ap.get_value('total_cost' ) l1_DF = ap.get_value('l1_DF' ) l2_DF = ap.get_value('l2_DF' ) print ("all_perms:" , all_perms, 'L2_m' , L2_m, 'L2_k' , L2_k, 'L2_n' , L2_n, 'L1_m' , L1_m, 'L1_k' , L1_k, 'L1_n' , L1_n, 'L0_m' , L0_m, 'L0_k' , L0_k, 'L0_n' , L0_n, 'total_cost' , total_cost, 'l1_DF' , l1_DF, 'l2_DF' , l2_DF) return (L2_m, L2_k, L2_n, L1_m, L1_k, L1_n, L0_m, L0_k, L0_n, total_cost) if __name__ == "__main__" : max_cost = 9999999 best_res = None best_perm = None for l2 in itertools.permutations(['m' , 'k' , 'n' ], 3 ): for l1 in itertools.permutations(['m' , 'k' , 'n' ], 3 ): res = solve_with_perms([l2, l1]) if res[-1 ] < max_cost: max_cost = res[-1 ] best_res = res best_perm = (l2, l1) print ("best perm: " , best_perm, "best tile: " , best_res)