Axe: A Simple Unified Layout Abstraction for Machine Learning Compilers

这篇论文是陈天奇团队的成果，提出一个统一的硬件感知抽象（Axe Layout），将逻辑张量坐标映射到多维物理空间，并设计基于此的多粒度、分布式感知的编译器DSL。今天就来解析一下Axe Layout的设计思路和实现细节。

核心公式

Axe Layout将逻辑张量索引映射到物理坐标集合：

\[L(x) = \{ D(x) + r + O \mid r \in R \}\]

其中： ### D (Shard) - 分片映射 - 是一个有序的iter列表 - 每个iter = (extent, stride, @axis) - extent: 硬件维度的逻辑大小 - stride: 相邻逻辑元素在硬件维度上的距离 - @axis: 物理轴的标签（device, warp, lane等） - 作用：将逻辑索引转换为物理坐标

R (Replica) - 复制维度

是一个集合（无序），独立于逻辑索引
格式：{axis_name: replica_count, ...}
作用：为并行执行添加额外维度
例如：4个线程独立执行相同的计算

O (Offset) - 偏移

固定的基地址或资源保留
格式：{axis_name: offset_value, ...}
例如：数据在内存中的起始位置、执行器件偏移

import numpy as np
import itertools
import pycute as cute
from typing import List, Tuple, Dict
from dataclasses import dataclass


@dataclass
class Iter:
  extent: int
  stride: int
  axis: str

  def __repr__(self):
    return f"({self.extent}, {self.stride}@{self.axis})"


@dataclass
class AxeLayout:
  D: List[Iter]
  R: List[Iter]
  O: Dict[str, int]

  def __repr__(self):
    d_str = " × ".join(map(str, self.D))
    r_str = " × ".join(map(str, self.R)) if self.R else "∅"
    o_str = ", ".join([f"{v}@{k}" for k, v in self.O.items()]) if self.O else "∅"
    return f"D: {d_str} | R: {r_str} | O: {o_str}"

  def print(self, name=""):
    if name:
      print(f"\n{name}:")

    if not self.D:
      d_extent_line = "( )"
      d_stride_line = "( )"
    else:
      col_widths = []
      for iter_obj in self.D:
        extent_str = str(iter_obj.extent)
        stride_str = f"{iter_obj.stride}@{iter_obj.axis}"
        col_width = max(len(extent_str), len(stride_str))
        col_widths.append(col_width)

      extent_parts = []
      for i, iter_obj in enumerate(self.D):
        extent_str = str(iter_obj.extent)
        padded = extent_str.center(col_widths[i])
        extent_parts.append(padded)
      d_extent_line = "( " + "  ".join(extent_parts) + " )"

      stride_parts = []
      for i, iter_obj in enumerate(self.D):
        stride_str = f"{iter_obj.stride}@{iter_obj.axis}"
        padded = stride_str.rjust(col_widths[i])
        stride_parts.append(padded)
      d_stride_line = "( " + ", ".join(stride_parts) + " )"

    if self.R:
      r_col_widths = []
      for iter_obj in self.R:
        extent_str = str(iter_obj.extent)
        stride_str = f"{iter_obj.stride}@{iter_obj.axis}"
        col_width = max(len(extent_str), len(stride_str))
        r_col_widths.append(col_width)

      r_extent_parts = []
      for i, iter_obj in enumerate(self.R):
        extent_str = str(iter_obj.extent)
        padded = extent_str.center(r_col_widths[i])
        r_extent_parts.append(padded)
      r_extent_line = "( " + "  ".join(r_extent_parts) + " )"

      r_stride_parts = []
      for i, iter_obj in enumerate(self.R):
        stride_str = f"{iter_obj.stride}@{iter_obj.axis}"
        padded = stride_str.rjust(r_col_widths[i])
        r_stride_parts.append(padded)
      r_stride_line = "( " + ", ".join(r_stride_parts) + " )"

      print(d_extent_line + "   " + r_extent_line)
      print(d_stride_line + " + " + r_stride_line, end="")
    else:
      print(d_extent_line)
      print(d_stride_line, end="")

    if self.O:
      o_items = [f"{offset}@{axis}" for axis, offset in self.O.items()]
      o_str = " + ".join(o_items)
      print(" + " + o_str, end="")

    print()

Examples

NVIDIA Tensor Core tile

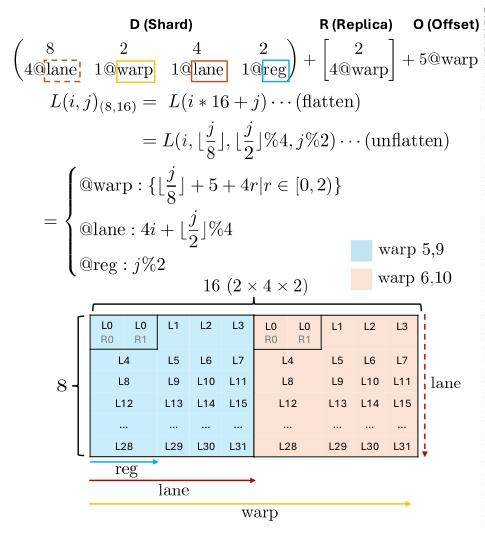
有了基础的定义后，我们可以尝试实现论文中的第一个例子，映射逻辑 \(8×16\) tile到GPU的2个warp（各32 lane）+ 2个寄存器：

\[\begin{pmatrix}8 & 2 & 4 & 2 \\ 4@\texttt{lane} & 1@\texttt{warp} & 1@\texttt{lane} & 1@\texttt{reg}\end{pmatrix} + \begin{bmatrix}2 \\ 4@\texttt{warp}\end{bmatrix} + 5@\texttt{warp}\]

layout_a = AxeLayout(D=[
    Iter(8, 4, "lane"),
    Iter(2, 1, "warp"),
    Iter(4, 1, "lane"),
    Iter(2, 1, "reg"),
],
    R=[Iter(2, 4, "warp")],
    O={"warp": 5})

layout_a.print("layout_a")

layout_a:
(   8       2       4       2   )   (   2    )
( 4@lane, 1@warp, 1@lane, 1@reg ) + ( 4@warp ) + 5@warp

Distributed sharding on a 2×2 GPU mesh

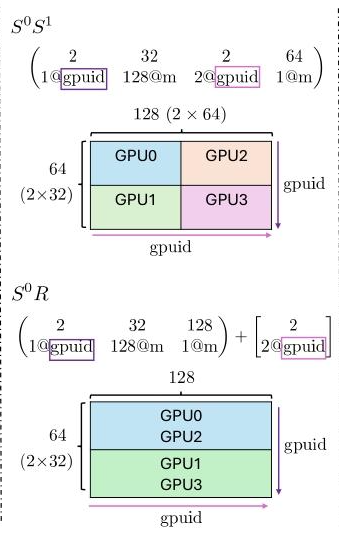
假设一个\(64×128\)张量在4个GPU上的分片+复制混合：

完全切分（行按GPU行，列按GPU列分）： \[\begin{pmatrix}2 & 32 & 2 & 64 \\ 1@\texttt{gpuid} & 128@\texttt{m} & 2@\texttt{gpuid} & 1@\texttt{m}\end{pmatrix}\]

这里的gpuid表示设备维度，这里的m表示内存维度，如果把内存维度的Iter单独抽取出来，就可以计算在每个设备中Local Tensor的Layout。把gpuid的Iter出来，可以用stride来隐式体现gpu mesh的分布方式。

行切分+列复制（行切分，每行shard复制到行内两GPU）： \[\begin{pmatrix}2 & 32 & 128 \\ 1@\texttt{gpuid} & 128@\texttt{m} & 1@\texttt{m}\end{pmatrix} + \begin{bmatrix}2 \\ 2@\texttt{gpuid}\end{bmatrix}\]

实际上这两个就是经典的分布式张量切分方式，对应到SBP里面分别为：

\[ \begin{aligned} (split(0), split(1)) \\ (split(0), broadcast) \end{aligned} \]

layout_b = AxeLayout(D=[
    Iter(2, 1, "gpuid"),
    Iter(32, 128, "m"),
    Iter(2, 2, "gpuid"),
    Iter(64, 1, "m")],
    R=[],
    O={})
layout_b.print("layout_b")

layout_b:
(    2       32      2      64 )
( 1@gpuid, 128@m, 2@gpuid, 1@m )

Native multidimensional memory in Accelerators

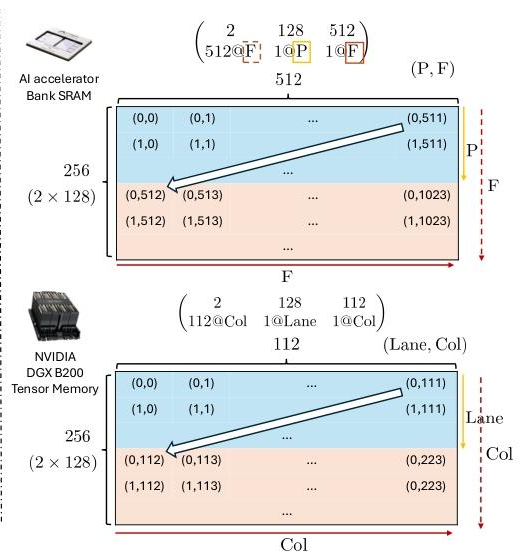
这里是对于物理内存硬件的映射，认为P是memory bank partitions, F为free dimensions。主要体现的是Axe Layout是同时支持并行硬件维度和存储硬件的表达，所以当不考虑并行维度时，可以完成传统layout的功能。

layout_c = AxeLayout(D=[
    Iter(2, 512, "F"),
    Iter(128, 1, "P"),
    Iter(512, 1, "F")],
    R=[],
    O={})

layout_d = AxeLayout(D=[
    Iter(2, 112, "Col"),
    Iter(128, 1, "Lane"),
    Iter(112, 1, "Col")],
    R=[],
    O={})

layout_c.print("layout_c")
layout_d.print("layout_d")

layout_c:
(   2    128  512 )
( 512@F, 1@P, 1@F )

layout_d:
(    2      128     112  )
( 112@Col, 1@Lane, 1@Col )

Forward Mapping

AxeLayout实际上是定义了logical index与hardware index的relation，基于此所实现的 logical index -> parallel index的映射称为forward mapping。

我这里拿第一个例子，具体计算前向过程。首先shard部分负责分解原始的logical index，而他的stride是应用于hardware axes的。而后replica则会扩展映射集合，和offset部分一起将偏移作用到hardware axes上。

logical coord: (i=2, j=9)
          ▼
shape: (8, 16)
          ▼
linear index: 2 * 16 + 9 = 41
          ▼
decomposed index as:
    > 41 ÷ 16 = 2
    > (41 % 16) ÷ 8 = 1
    > ((41 % 16) % 8) // 2 = 0
    > ((41 % 16) % 8) % 2 = 1
          ▼
shard coord:
    (  2   ,   1   ,   0   ,   1   )
          ▼
    (  8       2       4       2   )             (  2   )  
D = (4@lane, 1@warp, 1@lane, 1@reg)     +    R = (4@warp)    +    O = (5@warp)
          ▼
    > lane = 2*4 + 0*1 = 8                > warp0 = 0*4 = 0       >  warp = 5
    > warp = 1*1 = 1                      > warp1 = 1*4 = 4     
    > reg = 1*1 = 1                              
          ▼
  {lane: 8, warp: 1, reg: 1}            +  [{warp: 0}, {warp: 4}]  +   {warp: 5}
          ▼
offset = [
    {warp: 1+0+5 = 6 , lane: 8, reg: 1},
    {warp: 1+4+5 = 10, lane: 8, reg: 1}
]

上述流程也许有些抽象，我们可以通过代码来更直观地理解Axe Layout的前向计算过程。这里我复用了cute中的一些函数来辅助计算映射过程：


def forward(self: AxeLayout, coord: Tuple[int, ...], shape: Tuple[int, ...]):
  # 1. map layout to AxeLayout's shard
  shard_extents = tuple(i.extent for i in self.D)
  org_idx = cute.crd2idx(coord, shape, cute.suffix_product(shape))
  shard_crd = cute.idx2crd(org_idx, shard_extents[::-1])[::-1]  # reverse for correct order
  shards = [(idx * it.stride, it.axis) for (idx, it) in zip(shard_crd, self.D)]
  rep_set = []
  replica = self.R if len(self.R) else [Iter(1, 0, None)]
  for reps in itertools.product([(i * it.stride, it.axis) for it in replica for i in range(it.extent)]):
    d = dict()
    for val, axis in shards:  # D
      d[axis] = d.get(axis, 0) + val
    for val, axis in reps:  # R
      if axis is not None:
        d[axis] = d.get(axis, 0) + val
    for axis, val in self.O.items():  # O
      d[axis] = d.get(axis, 0) + val
    rep_set.append(d)

  return rep_set

接下来我们给定一个具体的logical coordinate (2, 9)，并通过Axe Layout的forward函数来计算映射到的并行轴坐标集合：

def pretty_print(crd: List[Dict[str, int]], **kwargs):
  key_order = dict()
  for k,v in kwargs.items():
    key_order[k] = v
  print([{k: d[k] for k in sorted(d, key=lambda k: key_order.get(k, 99))} for d in crd])

AxeLayout.forward = forward
hardware_coords = layout_a.forward((2, 9), (8, 16))

pretty_print(hardware_coords, warp=0, lane=1, reg=2)

[{'warp': 6, 'lane': 8, 'reg': 1}, {'warp': 10, 'lane': 8, 'reg': 1}]

Backward Mapping

Axe Layout同样支持从 hardware index -> logical index的映射过程，称为backward mapping。这个过程就会比之前稍微简单一些，因为不需要考虑replica的扩展，只需要将offset和shard的过程反过来即可。具体流程我就不赘述，直接给出代码：

def backward(self: AxeLayout, indices: List[Dict[str, int]], shape: Tuple[int, ...]):
  index = indices[0].copy()
  # 1. remove O
  for axis, offset in self.O.items():
    index[axis] = index.get(axis, 0) - offset
  # 2. skip R
  # 3. remove D
  shard_domains: Dict[str, List[Tuple[int, int, int]]] = {}
  for i, it in enumerate(self.D):
    sdomain = shard_domains.get(it.axis, ([]))
    sdomain.append((i, it.extent, it.stride))
    shard_domains[it.axis] = sdomain
  
  scoords = [-1] * len(self.D) 
  for axis, tps in shard_domains.items():
    tps.sort(key=lambda it: it[0])
    slayout = cute.Layout(tuple(tp[1] for tp in tps), tuple(tp[2] for tp in tps))
    sindex = index[axis]
    scrd = cute.idx2crd(sindex, slayout.shape, slayout.stride)
    for i, (idx, _, _) in enumerate(tps):
      scoords[idx] = scrd[i]
  
  shard_extents = tuple(it.extent for it in self.D)
  linear_idx = cute.crd2idx(tuple(scoords), shard_extents, cute.suffix_product(shard_extents))
  logical_coord = cute.idx2crd(linear_idx, shape, cute.suffix_product(shape))

  return logical_coord

我们逆推之前layout a的backward结果，可以检查backward的结果和forward给的输入是一致的：


AxeLayout.backward = backward

logical_coord = layout_a.backward(hardware_coords, (8, 16))
assert logical_coord == (2, 9)
print(logical_coord)

(2, 9)

总结

这篇论文里面还提到支持Tile，Slice等操作，实际上也都是可以复用cute Layout Algorithm来实现的，这里就不进一步展开了。同时还有一些编译器语法的前端支持，比如如何定义Tensor，Execution scopes，这些内容不是我关注的重点，也就不展开了。总的来说Axe Layout还是一个比较简洁且强大的张量布局抽象，他察觉到了在sharding的时候，实际上需要绑定tensor logical shape和hardware shape，因此可以把两部分放到一个Shard结构中进行统一处理，这样把parallel resource和memory resource都可以纳入同一个layout framework下进行处理，能在兼容原始layout的同时方便的扩展分布式能力。