机器学习编译概念科普
带大家建立一个对机器学习编译的基本概念.
什么是机器学习编译?
机器学习编译 (machine learning compilation, MLC) 是指,将机器学习算法从开发阶段,通过变换和优化算法,使其变成部署状态。
开发形式 是指我们在开发机器学习模型时使用的形式。典型的开发形式包括用 PyTorch、TensorFlow 或 JAX 等通用框架编写的模型描述,以及与之相关的权重。
部署形式 是指执行机器学习应用程序所需的形式。它通常涉及机器学习模型的每个步骤的支撑代码、管理资源(例如内存)的控制器,以及与应用程序开发环境的接口(例如用于 android 应用程序的 java API)。
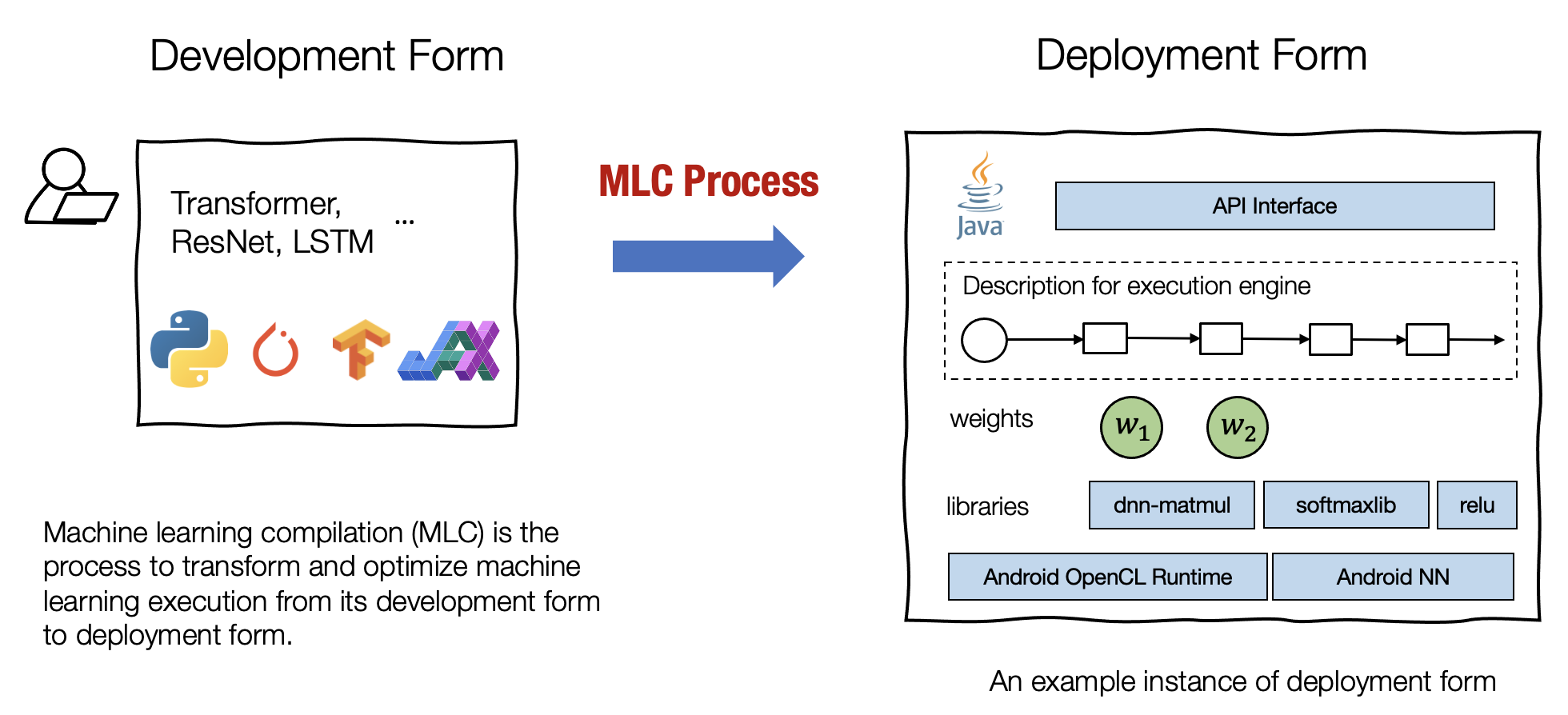
机器学习编译通常有以下几个目标:
集成与最小化依赖 部署过程通常涉及集成 (Integration),即将必要的元素组合在一起以用于部署应用程序。 例如,如果我们想启用一个安卓相机应用程序来检测猫,我们将需要图像分类模型的必要代码,但不需要模型无关的其他部分(例如,我们不需要包括用于 NLP 应用程序的embedding table)。代码集成、最小化依赖项的能力能够减小应用的大小,并且可以使应用程序部署到的更多的环境。
利用硬件加速 每个部署环境都有自己的一套原生加速技术,并且其中许多是专门为机器学习开发的。机器学习编译的一个目标就是是利用硬件本身的特性进行加速。 我们可以通过构建调用原生加速库的部署代码或生成利用原生指令(如 TensorCore)的代码来做到这一点。
通用优化 有许多等效的方法可以运行相同的模型执行。 MLC 的通用优化形式是不同形式的优化,以最小化内存使用或提高执行效率的方式转换模型执行。
这些目标没有严格的界限。例如,集成和硬件加速也可以被视为通用优化。根据具体的应用场景,我们可能对一些模型和生产环境对感兴趣,或者我们可能对部署到多个并选择最具成本效益的问题感兴趣。
重要的是,机器学习编译不一定表示单一稳定的解决方案。事实上,随着硬件和模型数量的增长,许多机器学习编译实践涉及与来自不同背景的开发人员的合作。硬件开发人员需要支持他们最新的硬件加速,机器学习工程师需要实现额外的优化,而同时算法工程师也引入了新模型。
机器学习编译中的关键要素
让我们首先回顾一个两层神经网络模型执行的例子。
在这个特定的模型中,我们通过展平输入图像中的像素来获取向量 (Vector);然后,我们应用线性变换,将输入图像投影到长度为 200 的向量上,并运行ReLU 激活函数。最后,我们将其映射到长度为 10 的向量,向量的每个元素对应于图像属于该特定类别的可能性大小。
张量 (Tensor) 是执行中最重要的元素。张量是表示神经网络模型执行的输入、输出和中间结果的多维数组。
张量函数 (Tensor functions) 神经网络的“知识”被编码在权重和接受张量和输出张量的计算序列中。我们将这些计算称为张量函数。值得注意的是,张量函数不需要对应于神经网络计算的单个步骤。部分计算或整个端到端计算也可以看作张量函数。
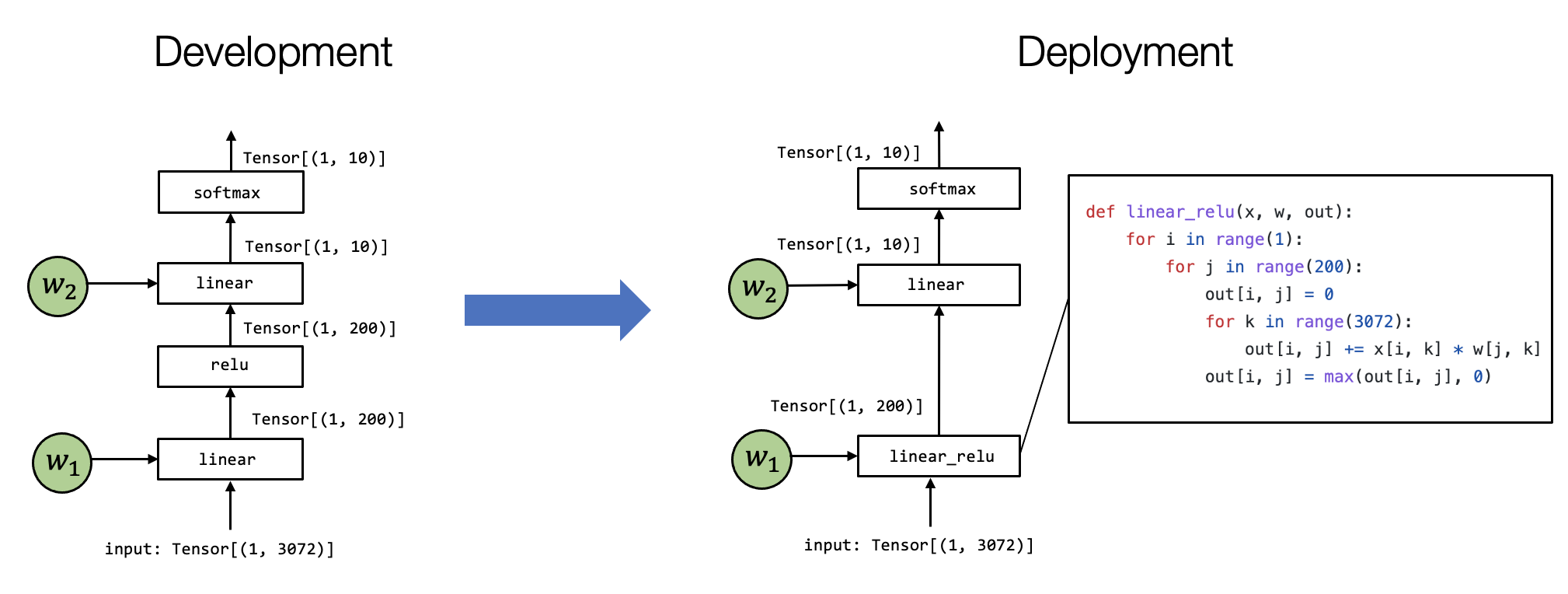
我们有多种方法可以在特定环境中实现模型执行。 上面的例子展示了一个例子。 值得注意的是,有两个区别: 首先,第一个linear层和relu计算被折叠成一个 linear_relu 函数,这需要有一个特定的linear_relu的详细实现。 当然,现实世界的用例,linear_relu 可以通过各种代码优化技术来实现,其中一些技术在的后面的课程中会进行介绍。 机器学习编译的过程就是是将上图左侧的内容转换为右侧的过程。在不同的场景中,这个过程可以是手动完成的,也可以使用一些自动转换工具,或两者兼而有之。
元张量函数
在上一章的概述中,我们介绍到机器学习编译的过程可以被看作张量函数之间的变换。一个典型的机器学习模型的执行包含许多步将输入张量之间转化为最终预测的计算步骤,其中的每一步都被称为元张量函数 (primitive tensor function)。

在上面这张图中,张量算子 linear, add, relu 和 softmax 均为元张量函数。特别的是,许多不同的抽象能够表示(和实现)同样的元张量函数(正如下图所示)。我们可以选择调用已经预先编译的框架库(如 torch.add 和 numpy.add)并利用在 Python 中的实现。在实践中,元张量函数被例如 C 或 C++ 的低级语言所实现,并且在一些时候会包含一些汇编代码。

许多机器学习框架都提供机器学习模型的编译过程,以将元张量函数变换为更加专门的、针对特定工作和部署环境的函数。
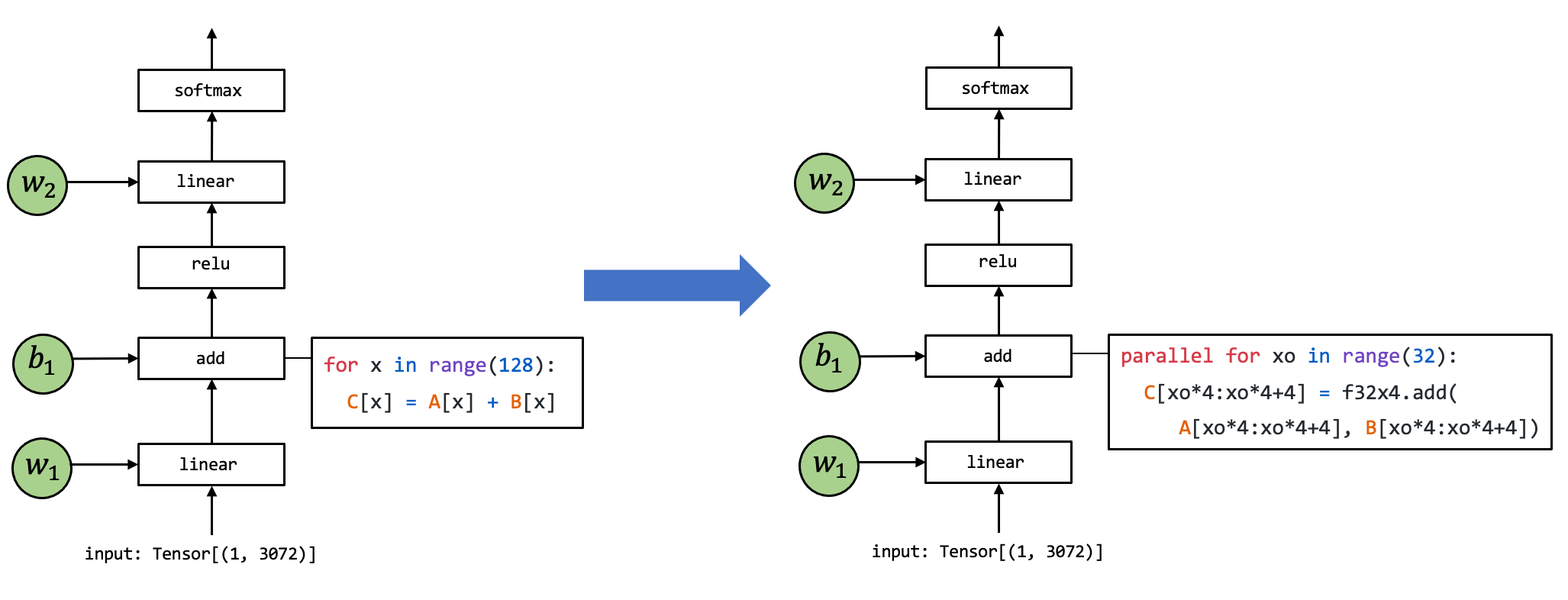
上面这张图展示了一个元张量函数 add 的实现被变换至另一个不同实现的例子,其中在右侧的代码是一段表示可能的组合优化的伪代码:左侧代码中的循环被拆分出长度为 4 的单元,f32x4.add 对应的是一个特殊的执行向量加法计算的函数。
张量程序抽象
上一节谈到了对元张量函数变换的需要。为了让我们能够更有效地变换元张量函数,我们需要一个有效的抽象来表示这些函数。
通常来说,一个典型的元张量函数实现的抽象包含了以下成分:存储数据的多维数组,驱动张量计算的循环嵌套以及计算部分本身的语句。
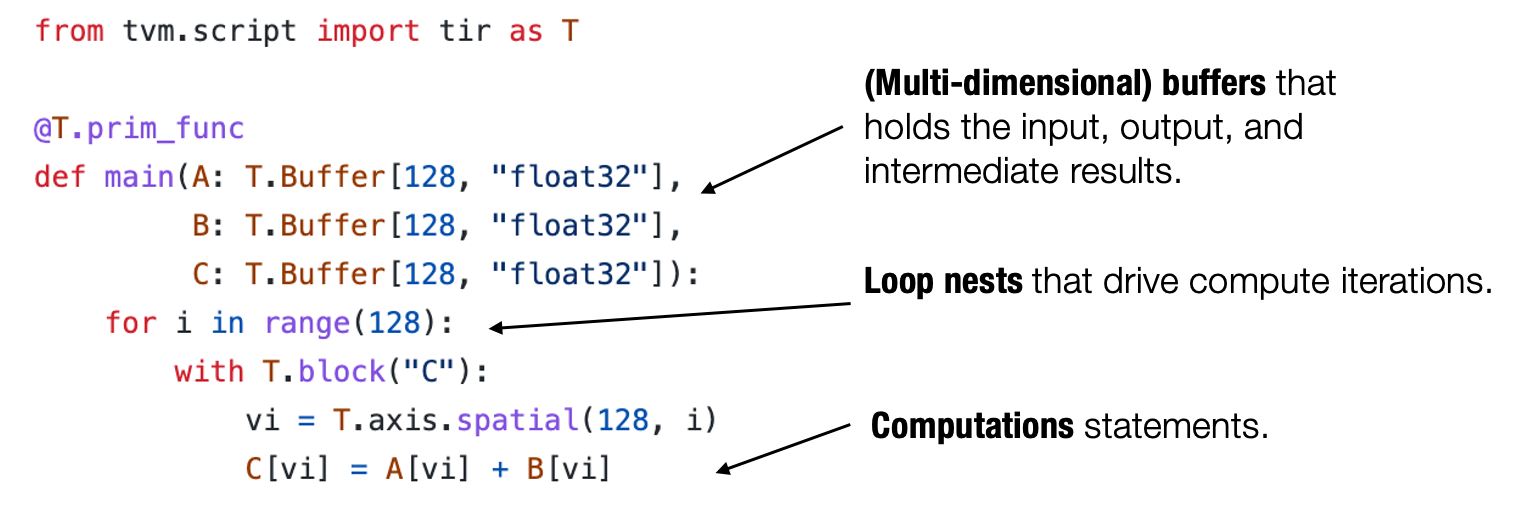
我们称这类抽象为张量程序抽象。张量程序抽象的一个重要性质是,他们能够被一系列有效的程序变换所改变。
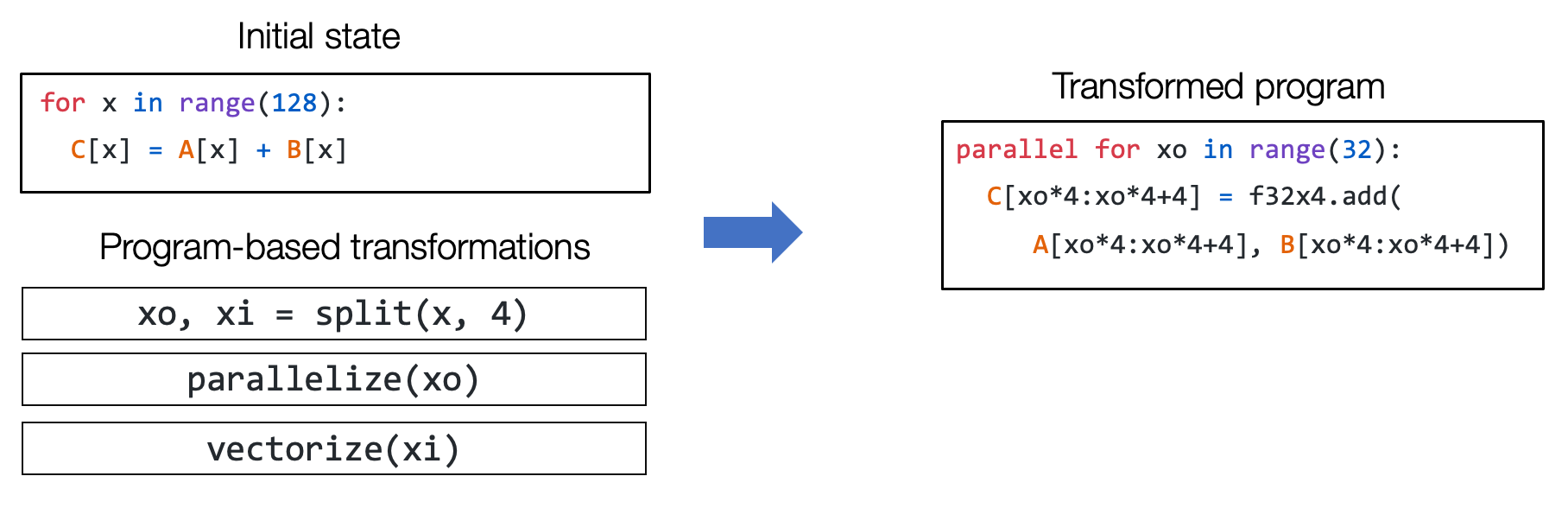
例如,我们能够通过一组变换操作(如循环拆分、并行和向量化)将上图左侧的一个初始循环程序变换为右侧的程序。
张量程序抽象中的其它结构
重要的是,我们不能任意地对程序进行变换,比方说这可能是因为一些计算会依赖于循环之间的顺序。但幸运的是,我们所感兴趣的大多数元张量函数都具有良好的属性(例如循环迭代之间的独立性)。
张量程序可以将这些额外的信息合并为程序的一部分,以使程序变换更加便利。

举个例子,上面图中的程序包含额外的 T.axis.spatial 标注,表明 vi 这个特定的变量被映射到循环变量 i,并且所有的迭代都是独立的。这个信息对于执行这个程序而言并非必要,但会使得我们在变换这个程序时更加方便。在这个例子中,我们知道我们可以安全地并行或者重新排序所有与 vi 有关的循环,只要实际执行中 vi 的值按照从 0 到 128 的顺序变化。
总结
- 元张量函数表示机器学习模型计算中的单个单元计算。
- 一个机器学习编译过程可以有选择地转换元张量函数的实现。
- 张量程序是一个表示元张量函数的有效抽象。
- 关键成分包括: 多维数组,循环嵌套,计算语句。
- 程序变换可以被用于加速张量程序的执行。
- 张量程序中额外的结构能够为程序变换提供更多的信息。
张量优化的程序变换方法
当我们在谈“优化”的时候,我们的目标是什么?如何通过“优化操作”,得到性能的提升呢?要解答这些疑问,我们需要了解硬件的基础的体系结构,了解硬件如何工作,才能在软件上实现算法的时候,尽可能去考虑利用硬件的一些特性,来做到高效的、极致的优化。 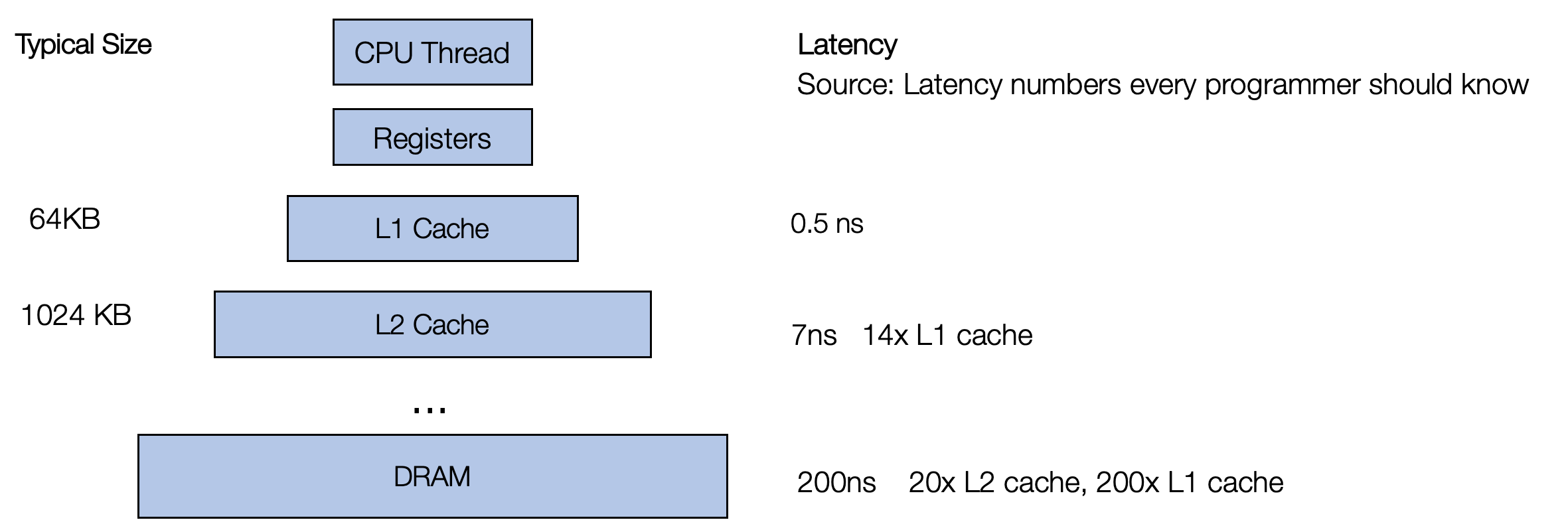
上图是典型的存储理器层次结构:主存容量大,访问速度慢,寄存器和缓存读取速度快,但容量有限。在寄存器的层级上,CPU可以在一个时钟周期内访问它们,如果CPU去访问外部的DDR的话,延迟是非常大的,大概是200个时钟周期左右。如果CPU去访问cache的话,一般需要6到12个cycle就够了。 所以,两个重要的优化宗旨:
优化内存访问: 充分利用寄存器和高速缓存去存数据。
提高并行性: 充分利用SIMD进行指令向量化和多核心并行.
接下来我们定义一个简单的例子, 两个matmul之间有一个elemwise的操作:
A = torch.empty((M, K), requires_grad=False, name='A')
B = torch.empty((K, L), requires_grad=False, name='B')
C = torch.matmul(A, B)
D = torch.exp(C)
E = torch.empty((L, N), requires_grad=False, name='E')
F = torch.matmul(D, E)我们将使用tvm把上述计算过程描述为tenor function, 并使用tvm的调度原语进行程序变换. 大家可以通过pip安装tvm来一起上手执行接下来的代码:
python3 -m pip install mlc-ai-nightly -f https://mlc.ai/wheelsimport tvm
from tvm import te
from tvm import tir
import numpy as np
from tvm.script import ir as I
from tvm.script import tir as T
M = 1024
K = 2048
L = 1024
N = 3072
A = te.placeholder((M, K), name='A')
B = te.placeholder((K, L), name='B')
rk = te.reduce_axis((0, K), name='rk')
C = te.compute((M, L), lambda m, l: te.sum(A[m, rk] * B[rk, l], axis=[rk]), name='C')
D = te.compute((M, L), lambda m, l: te.exp(C[m, l]), name='D')
E = te.placeholder((L, N), name='E')
rl = te.reduce_axis((0, L), name='rl')
F = te.compute((M, N), lambda m, n: te.sum(D[m, rl] * E[rl, n], axis=[rl]), name='F')
tir_sch: te.Schedule = te.create_schedule([C.op, D.op, F.op])
tvm.lower(tir_sch, [A, B, E]).show()# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32")):
T.func_attr({"from_legacy_te_schedule": T.bool(True), "tir.noalias": T.bool(True)})
C = T.allocate([1048576], "float32", "global")
F = T.allocate([3145728], "float32", "global")
C_1 = T.Buffer((1048576,), data=C)
for m, l in T.grid(1024, 1024):
C_1[m * 1024 + l] = T.float32(0.0)
for rk in range(2048):
cse_var_1: T.int32 = m * 1024 + l
A_1 = T.Buffer((2097152,), data=A.data)
B_1 = T.Buffer((2097152,), data=B.data)
C_1[cse_var_1] = C_1[cse_var_1] + A_1[m * 2048 + rk] * B_1[rk * 1024 + l]
C_2 = T.Buffer((1048576,), data=C)
for m, l in T.grid(1024, 1024):
cse_var_2: T.int32 = m * 1024 + l
C_2[cse_var_2] = T.exp(C_1[cse_var_2])
for m, n in T.grid(1024, 3072):
F_1 = T.Buffer((3145728,), data=F)
F_1[m * 3072 + n] = T.float32(0.0)
for rl in range(1024):
cse_var_3: T.int32 = m * 3072 + n
E_1 = T.Buffer((3145728,), data=E.data)
F_1[cse_var_3] = F_1[cse_var_3] + C_2[m * 1024 + rl] * E_1[rl * 3072 + n]
我们来先测试未经优化的程序执行速度:
a_nd = tvm.nd.array(np.random.randn(M, K).astype(np.float32))
b_nd = tvm.nd.array(np.random.randn(K, L).astype(np.float32))
e_nd = tvm.nd.array(np.random.randn(L, N).astype(np.float32))
rt_lib = tvm.build(tir_sch, [A, B, E], target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu(), number=3)
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd).mean} sec")Time cost of transformed sch.mod 6.2369096530000006 sec优化内存访问
考虑matmul的native实现时, 在机器上是这样执行的:
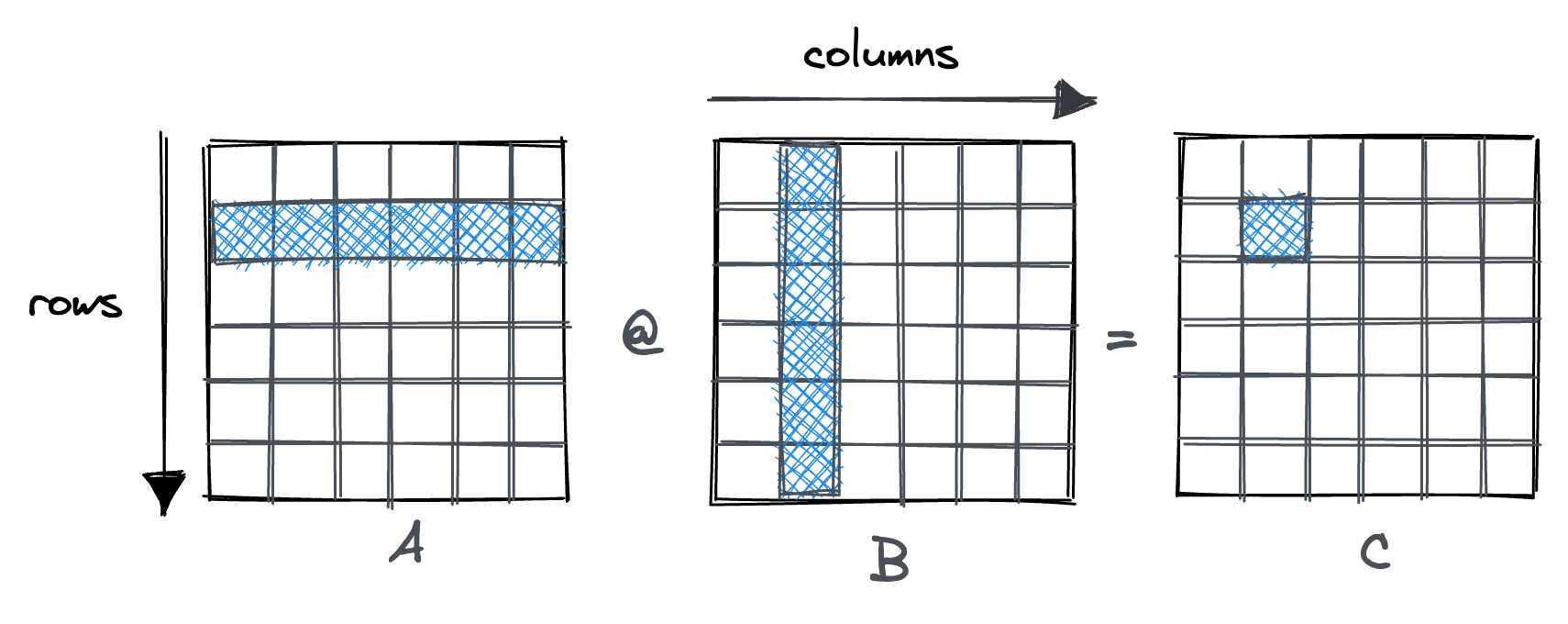
通常,处理器使用固定大小的cache line(通常为 64 字节)从内存加载数据。当迭代 A 的行时,我们在第一个条目上发生了缓存未命中。处理器的高速缓存行提取也将在其中保存接下来的 15 个浮点数,这是对高速缓存的良好利用。 然而,对于矩阵 B,我们沿着列走,每一步都会发生cache miss, 这个就产生了严重的内存开销.
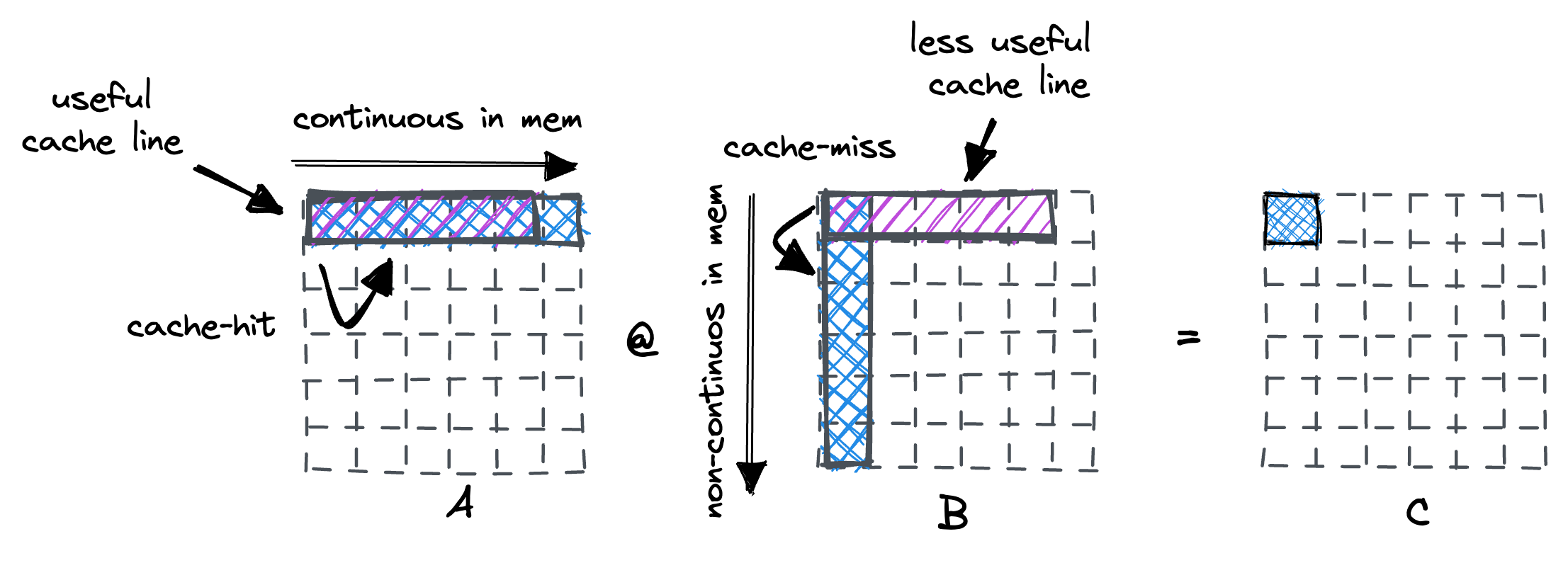
1. loop reorder
为了解决对于B矩阵的非连续访问导致的cache miss问题, 我们重新排序了两个矩阵乘的循环, 改变对于B矩阵的访问顺序.
tir_sch: te.Schedule = te.create_schedule([C.op, D.op, F.op])
m,l = C.op.axis
(k,) = C.op.reduce_axis
tir_sch[C].reorder(m,k,l)
m,n = F.op.axis
(l,) = F.op.reduce_axis
tir_sch[F].reorder(m,l,n)
rt_lib = tvm.build(tir_sch, [A, B, E], target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd).mean} sec")
tvm.lower(tir_sch, [A, B, E]).show()Time cost of transformed sch.mod 0.4165279375 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32")):
T.func_attr({"from_legacy_te_schedule": T.bool(True), "tir.noalias": T.bool(True)})
C = T.allocate([1048576], "float32", "global")
F = T.allocate([3145728], "float32", "global")
C_1 = T.Buffer((1048576,), data=C)
for m in range(1024):
for l_init in range(1024):
C_1[m * 1024 + l_init] = T.float32(0.0)
for rk, l in T.grid(2048, 1024):
cse_var_1: T.int32 = m * 1024 + l
A_1 = T.Buffer((2097152,), data=A.data)
B_1 = T.Buffer((2097152,), data=B.data)
C_1[cse_var_1] = C_1[cse_var_1] + A_1[m * 2048 + rk] * B_1[rk * 1024 + l]
C_2 = T.Buffer((1048576,), data=C)
for m, l in T.grid(1024, 1024):
cse_var_2: T.int32 = m * 1024 + l
C_2[cse_var_2] = T.exp(C_1[cse_var_2])
for m in range(1024):
F_1 = T.Buffer((3145728,), data=F)
for n_init in range(3072):
F_1[m * 3072 + n_init] = T.float32(0.0)
for rl, n in T.grid(1024, 3072):
cse_var_3: T.int32 = m * 3072 + n
E_1 = T.Buffer((3145728,), data=E.data)
F_1[cse_var_3] = F_1[cse_var_3] + C_2[m * 1024 + rl] * E_1[rl * 3072 + n]
2. tiling
可以发现仅通过loop reorder就可以让执行速度提升10倍. 虽然现在每一次load的cache miss减少了, 但是考虑整个的矩阵乘执行过程:
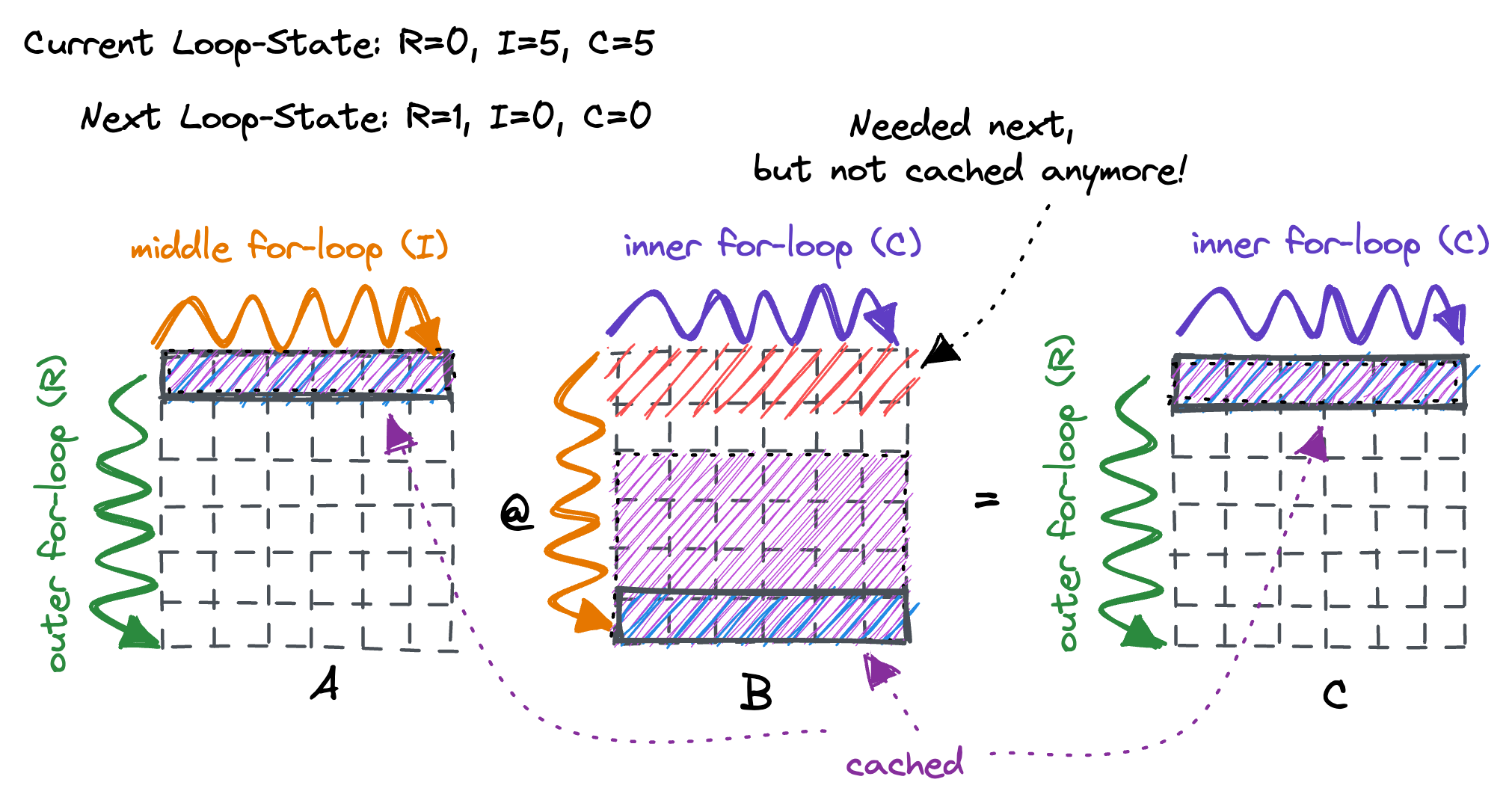
目前的计算模式是固定A矩阵的一行, 然后反复加载B矩阵的所有行, 但是考虑到cache如果为32kb时, 在这个例子中只能缓存2=32*1024/4/4096行的B矩阵, 那么也就是最多两行之后就后来的B矩阵数据就会将之前cache中存储的数据驱除出去, 为了解决这个问题, 我们的方法就是通过切分K循环, 让他分为多个block, 使得每个block内部的B矩阵将会被缓存在cache中:
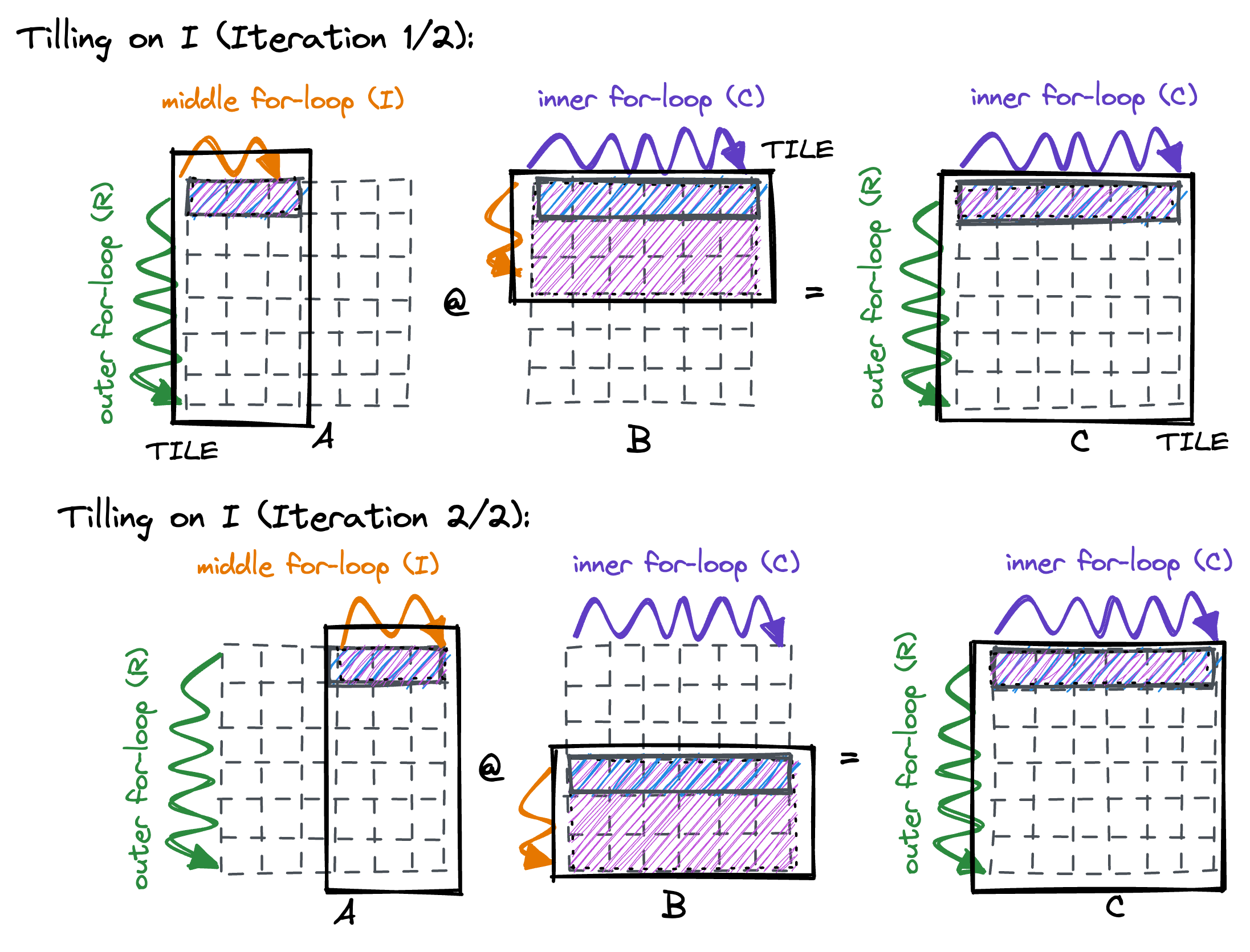
tir_sch: te.Schedule = te.create_schedule([C.op, D.op, F.op])
m, l = C.op.axis
(k,) = C.op.reduce_axis
ko, ki = tir_sch[C].split(k, 8)
tir_sch[C].reorder(ko, m, ki, l)
m, n = F.op.axis
(l,) = F.op.reduce_axis
lo, li = tir_sch[F].split(l, 8)
tir_sch[F].reorder(lo, m, li, n)
rt_lib = tvm.build(tir_sch, [A, B, E], target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd).mean} sec")
tvm.lower(tir_sch, [A, B, E]).show()Time cost of transformed sch.mod 0.3838193083 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32")):
T.func_attr({"from_legacy_te_schedule": T.bool(True), "tir.noalias": T.bool(True)})
C = T.allocate([1048576], "float32", "global")
F = T.allocate([3145728], "float32", "global")
C_1 = T.Buffer((1048576,), data=C)
for m_init, l_init in T.grid(1024, 1024):
C_1[m_init * 1024 + l_init] = T.float32(0.0)
for rk_outer, m, rk_inner, l in T.grid(256, 1024, 8, 1024):
cse_var_1: T.int32 = m * 1024 + l
A_1 = T.Buffer((2097152,), data=A.data)
B_1 = T.Buffer((2097152,), data=B.data)
C_1[cse_var_1] = C_1[cse_var_1] + A_1[m * 2048 + rk_outer * 8 + rk_inner] * B_1[rk_outer * 8192 + rk_inner * 1024 + l]
C_2 = T.Buffer((1048576,), data=C)
for m, l in T.grid(1024, 1024):
cse_var_2: T.int32 = m * 1024 + l
C_2[cse_var_2] = T.exp(C_1[cse_var_2])
F_1 = T.Buffer((3145728,), data=F)
for m_init, n_init in T.grid(1024, 3072):
F_1[m_init * 3072 + n_init] = T.float32(0.0)
for rl_outer, m, rl_inner, n in T.grid(128, 1024, 8, 3072):
cse_var_3: T.int32 = m * 3072 + n
E_1 = T.Buffer((3145728,), data=E.data)
F_1[cse_var_3] = F_1[cse_var_3] + C_2[m * 1024 + rl_outer * 8 + rl_inner] * E_1[rl_outer * 24576 + rl_inner * 3072 + n]
可以发现虽然对reduce维度添加了tiling,但是最终的性能没有什么提升. 那是因为要考虑A/B/C矩阵都存储在cache中时, 很有可能B矩阵的一行都无法完全缓存起来, 因此实施tiling优化时通常是多个维度同时进行的:
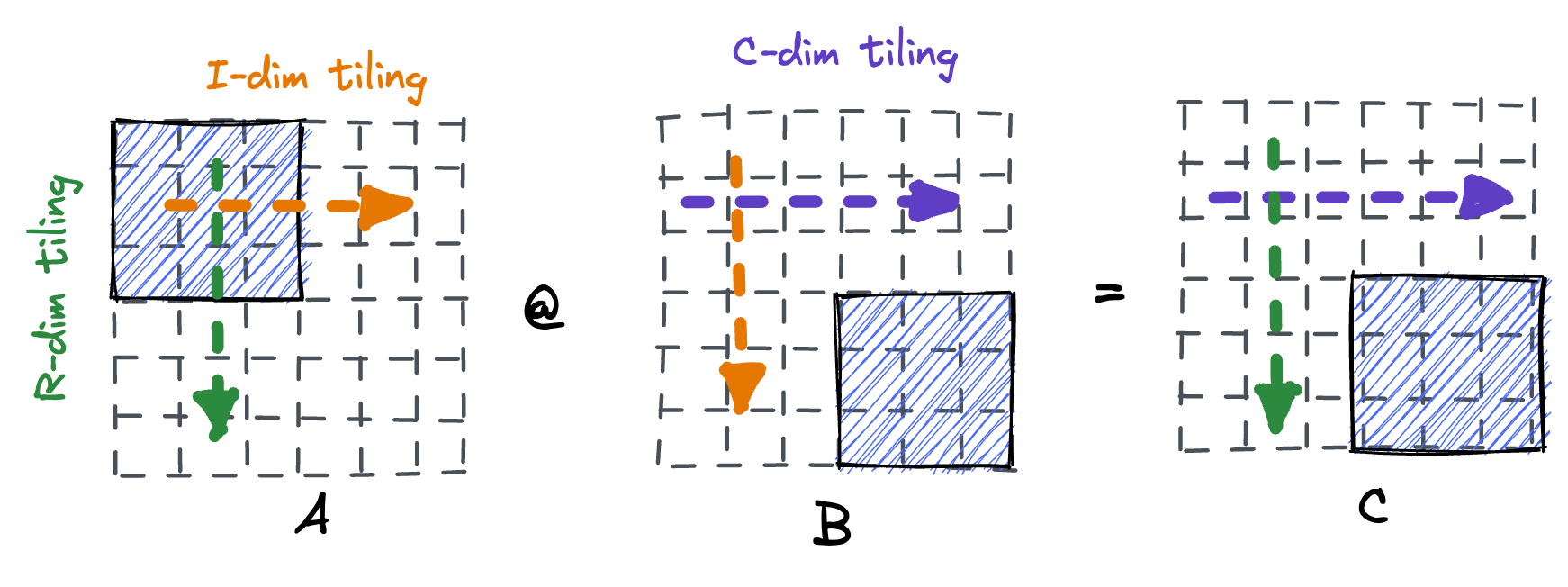
tir_sch: te.Schedule = te.create_schedule([C.op, D.op, F.op])
m, l = C.op.axis
(k,) = C.op.reduce_axis
mo, mi = tir_sch[C].split(m, 16)
ko, ki = tir_sch[C].split(k, 8)
lo, li = tir_sch[C].split(l, 8)
tir_sch[C].reorder(mo, lo, ko, mi, ki, li)
m, n = F.op.axis
(l,) = F.op.reduce_axis
mo, mi = tir_sch[F].split(m, 16)
lo, li = tir_sch[F].split(l, 8)
no, ni = tir_sch[F].split(n, 8)
tir_sch[F].reorder(mo, no, lo, mi, li, ni)
rt_lib = tvm.build(tir_sch, [A, B, E], target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd).mean} sec")
tvm.lower(tir_sch, [A, B, E]).show()Time cost of transformed sch.mod 0.3760715791 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32")):
T.func_attr({"from_legacy_te_schedule": T.bool(True), "tir.noalias": T.bool(True)})
C = T.allocate([1048576], "float32", "global")
F = T.allocate([3145728], "float32", "global")
C_1 = T.Buffer((1048576,), data=C)
for m_outer, l_outer in T.grid(64, 128):
for m_inner_init, l_inner_init in T.grid(16, 8):
C_1[m_outer * 16384 + m_inner_init * 1024 + l_outer * 8 + l_inner_init] = T.float32(0.0)
for rk_outer, m_inner, rk_inner, l_inner in T.grid(256, 16, 8, 8):
cse_var_2: T.int32 = l_outer * 8
cse_var_1: T.int32 = m_outer * 16384 + m_inner * 1024 + cse_var_2 + l_inner
A_1 = T.Buffer((2097152,), data=A.data)
B_1 = T.Buffer((2097152,), data=B.data)
C_1[cse_var_1] = C_1[cse_var_1] + A_1[m_outer * 32768 + m_inner * 2048 + rk_outer * 8 + rk_inner] * B_1[rk_outer * 8192 + rk_inner * 1024 + cse_var_2 + l_inner]
C_2 = T.Buffer((1048576,), data=C)
for m, l in T.grid(1024, 1024):
cse_var_3: T.int32 = m * 1024 + l
C_2[cse_var_3] = T.exp(C_1[cse_var_3])
for m_outer, n_outer in T.grid(64, 384):
F_1 = T.Buffer((3145728,), data=F)
for m_inner_init, n_inner_init in T.grid(16, 8):
F_1[m_outer * 49152 + m_inner_init * 3072 + n_outer * 8 + n_inner_init] = T.float32(0.0)
for rl_outer, m_inner, rl_inner, n_inner in T.grid(128, 16, 8, 8):
cse_var_5: T.int32 = n_outer * 8
cse_var_4: T.int32 = m_outer * 49152 + m_inner * 3072 + cse_var_5 + n_inner
E_1 = T.Buffer((3145728,), data=E.data)
F_1[cse_var_4] = F_1[cse_var_4] + C_2[m_outer * 16384 + m_inner * 1024 + rl_outer * 8 + rl_inner] * E_1[rl_outer * 24576 + rl_inner * 3072 + cse_var_5 + n_inner]
3. loop fusion
loop fusion是将两个循环中的语句放到一起, 减少对于同一个数据的重用距离, 增加了数据的局部性, 考虑我们的例子中, 当矩阵C计算结束后才能开始下一个exp的计算, 这个时候原本访问到最后一行的数据又被推出cache中重新加载第一行的数据. 此时时候可以把exp的计算放在第一个matmul的tile计算结束后立即计算.
但是因为tvm的中缺少更加详细的分析, 导致某些合法的调度并没有被tvm te(tensor expression)的调度原语所支持, 因此接下来采用tvm后来提出Tensor IR抽象, 在tir中提供了比te(tensor expression)中更多的调度方式, 比如reindex/cache_index/merge/decompose_reduction等方法, 当无法通过调度原语来达到想要的优化变化时甚至可以直接通过手写的方法来支持.
接下来先将前面的te抽象转换为tir抽象:
prim_func = te.create_prim_func([A, B, E, F])
prim_func.show()# from tvm.script import tir as T
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m, l, rk in T.grid(1024, 1024, 2048):
with T.block("C"):
v_m, v_l, v_rk = T.axis.remap("SSR", [m, l, rk])
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m, l in T.grid(1024, 1024):
with T.block("D"):
v_m, v_l = T.axis.remap("SS", [m, l])
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for m, n, rl in T.grid(1024, 3072, 1024):
with T.block("F"):
v_m, v_n, v_rl = T.axis.remap("SSR", [m, n, rl])
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
tir中以block为单位来调度源代码, 这里通过tir来实现和之前te中相同的调度策略:
f_nd = tvm.nd.empty((M, N), dtype="float32")tir_sch = tir.Schedule(prim_func)
m, l, k = tir_sch.get_loops('C')
mo, mi = tir_sch.split(m, [M // 16, 16])
ko, ki = tir_sch.split(k, [K // 8, 8])
lo, li = tir_sch.split(l, [L // 8, 8])
tir_sch.reorder(mo, lo, ko, mi, ki, li)
m, n, l = tir_sch.get_loops('F')
mo, mi = tir_sch.split(m, [M // 16, 16])
lo, li = tir_sch.split(l, [L // 8, 8])
no, ni = tir_sch.split(n, [N // 8, 8])
tir_sch.reorder(mo, no, lo, mi, li, ni)
rt_lib = tvm.build(tir_sch.mod, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")
tir_sch.mod.show()Time cost of transformed sch.mod 1.0223547624999998 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m_0, l_0, rk_0, m_1, rk_1, l_1 in T.grid(64, 128, 256, 16, 8, 8):
with T.block("C"):
v_m = T.axis.spatial(1024, m_0 * 16 + m_1)
v_l = T.axis.spatial(1024, l_0 * 8 + l_1)
v_rk = T.axis.reduce(2048, rk_0 * 8 + rk_1)
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m, l in T.grid(1024, 1024):
with T.block("D"):
v_m, v_l = T.axis.remap("SS", [m, l])
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for m_0, n_0, rl_0, m_1, rl_1, n_1 in T.grid(64, 384, 128, 16, 8, 8):
with T.block("F"):
v_m = T.axis.spatial(1024, m_0 * 16 + m_1)
v_n = T.axis.spatial(3072, n_0 * 8 + n_1)
v_rl = T.axis.reduce(1024, rl_0 * 8 + rl_1)
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
这里可以发现相同调度下, tir速度慢了许多, 这是由于tir的函数默认将init操作放到循环内部导致的, 我们暂时忽略这个问题. 只关注通过fusion之后是否能产生性能提升:
mo, lo, ko, mi, ki, li = tir_sch.get_loops('C')
m1, l1 = tir_sch.get_loops('D')
m1o, m1i = tir_sch.split(m1, [M // 16, 16])
l1o, l1i = tir_sch.split(l1, [L // 8, 8])
tir_sch.reorder(m1o, l1o, m1i, l1i)
tir_sch.merge(lo, l1o)
rt_lib = tvm.build(tir_sch.mod, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")
tir_sch.mod.show()Time cost of transformed sch.mod 0.8789533792 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m_0_m, l_0_m in T.grid(64, 128):
for rk_0, m_1, rk_1, l_1 in T.grid(256, 16, 8, 8):
with T.block("C"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_l = T.axis.spatial(1024, l_0_m * 8 + l_1)
v_rk = T.axis.reduce(2048, rk_0 * 8 + rk_1)
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m_1, l_1 in T.grid(16, 8):
with T.block("D"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_l = T.axis.spatial(1024, l_0_m * 8 + l_1)
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for m_0, n_0, rl_0, m_1, rl_1, n_1 in T.grid(64, 384, 128, 16, 8, 8):
with T.block("F"):
v_m = T.axis.spatial(1024, m_0 * 16 + m_1)
v_n = T.axis.spatial(3072, n_0 * 8 + n_1)
v_rl = T.axis.reduce(1024, rl_0 * 8 + rl_1)
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
可以发现通过fusion elemwise的操作有微弱的速度提升. 其实还有更加激进的fusion, 这个例子中还可以合并两个matmul的m循环. 虽然合并两个循环的m循环是一个合法的优化, 但通过tir去merge是会触发错误的, 因此这里通过手动修改代码的方式来实现这个调度:
from tvm.script import ir as I
from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m_0_m in T.grid(64):
for l_0_m in T.grid(128):
for rk_0, m_1, rk_1, l_1 in T.grid(256, 16, 8, 8):
with T.block("C"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_l = T.axis.spatial(1024, l_0_m * 8 + l_1)
v_rk = T.axis.reduce(2048, rk_0 * 8 + rk_1)
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m_1, l_1 in T.grid(16, 8):
with T.block("D"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_l = T.axis.spatial(1024, l_0_m * 8 + l_1)
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for n_0, rl_0, m_1, rl_1, n_1 in T.grid(384, 128, 16, 8, 8):
with T.block("F"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_n = T.axis.spatial(3072, n_0 * 8 + n_1)
v_rl = T.axis.reduce(1024, rl_0 * 8 + rl_1)
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
rt_lib = tvm.build(Module, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")Time cost of transformed sch.mod 0.792521475 sec其实还有更多的优化手段, 但是在tensor ir不方便实现, 比如通过lift allocation + stage memory + add guard的方式来实现在外层循环申请buffer,并在内循环中逐步填充,并在此后的迭代中重复使用, 但目前还是只能通过手动修改tir代码来实现. 最近有一另个调度抽象exo-lang提供了这些调度手段.
提高并行性
现在只考虑单核的程序, 提升并行性通常就使用simd加速:
tir_sch = tir.Schedule(Module)
(*_, li) = tir_sch.get_loops('C')
tir_sch.vectorize(li)
(*_, ni) = tir_sch.get_loops('F')
tir_sch.vectorize(ni)
rt_lib = tvm.build(tir_sch.mod, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")
tir_sch.mod.show()Time cost of transformed sch.mod 0.2236641083 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m_0_m in range(64):
for l_0_m in range(128):
for rk_0, m_1, rk_1 in T.grid(256, 16, 8):
for l_1 in T.vectorized(8):
with T.block("C"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_l = T.axis.spatial(1024, l_0_m * 8 + l_1)
v_rk = T.axis.reduce(2048, rk_0 * 8 + rk_1)
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m_1, l_1 in T.grid(16, 8):
with T.block("D"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_l = T.axis.spatial(1024, l_0_m * 8 + l_1)
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for n_0, rl_0, m_1, rl_1 in T.grid(384, 128, 16, 8):
for n_1 in T.vectorized(8):
with T.block("F"):
v_m = T.axis.spatial(1024, m_0_m * 16 + m_1)
v_n = T.axis.spatial(3072, n_0 * 8 + n_1)
v_rl = T.axis.reduce(1024, rl_0 * 8 + rl_1)
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
自动程序优化
前面讨论了有许多不同的方法可以变换同一个程序, 但是由于方法多样且每个方法还存在各种参数, 通过手动优化要求开发者对于硬件架构有比较深入的理解, 因此催生了自动化优化的需求.
首先回顾一下之前的调度方法, 假设我们将调度方法封装成为一个函数:
def schedule_mm(tir_sch: tvm.tir.Schedule, jfactor=4):
m, l, k = tir_sch.get_loops('C')
mo, mi = tir_sch.split(m, [None, 16])
ko, ki = tir_sch.split(k, [None, 8])
lo, li = tir_sch.split(l, [None, 8])
tir_sch.reorder(mo, lo, ko, mi, ki, li)
return tir_sch
prim_func = te.create_prim_func([A, B, E, F])
tir_sch = tvm.tir.Schedule(prim_func)
tir_sch = schedule_mm(tir_sch)
rt_lib = tvm.build(tir_sch.mod, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")
tir_sch.mod.show()Time cost of transformed sch.mod 6.0141817167 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m_0, l_0, rk_0, m_1, rk_1, l_1 in T.grid(64, 128, 256, 16, 8, 8):
with T.block("C"):
v_m = T.axis.spatial(1024, m_0 * 16 + m_1)
v_l = T.axis.spatial(1024, l_0 * 8 + l_1)
v_rk = T.axis.reduce(2048, rk_0 * 8 + rk_1)
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m, l in T.grid(1024, 1024):
with T.block("D"):
v_m, v_l = T.axis.remap("SS", [m, l])
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for m, n, rl in T.grid(1024, 3072, 1024):
with T.block("F"):
v_m, v_n, v_rl = T.axis.remap("SSR", [m, n, rl])
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
除了 sch.mod, tir.Schedule 提供的另一个数据结构是历史轨迹 (trace), 它包含了 IRModule 在变换过程中所涉及的步骤. 我们可以使用以下代码将其打印出来:
print(tir_sch.trace)# from tvm import tir
def apply_trace(sch: tir.Schedule) -> None:
b0 = sch.get_block(name="C", func_name="main")
l1, l2, l3 = sch.get_loops(block=b0)
l4, l5 = sch.split(loop=l1, factors=[None, 16], preserve_unit_iters=True, disable_predication=False)
l6, l7 = sch.split(loop=l3, factors=[None, 8], preserve_unit_iters=True, disable_predication=False)
l8, l9 = sch.split(loop=l2, factors=[None, 8], preserve_unit_iters=True, disable_predication=False)
sch.reorder(l4, l8, l6, l5, l7, l9)上面的历史轨迹与我们在 schedule_mm 中指定的变换一致. 需要注意的一点是, 历史轨迹加上原始程序一起, 为我们提供了一种能够完全重新生成最终输出程序的方法. 记住这一点,我们将在本章中使用历史轨迹作为检查变换的另一种方式.
随机调度变换
假设我们知道想要对原始 TensorIR 程序进行哪些变换, 并且其中一些变化的参数基于我们对底层环境的理解,例如缓存和硬件单元. 因此, 我们想指定调度的方式, 但是选择调度的一些参数这样省略一些细节. 一种自然方法是在我们的变换中添加一些随机元素, 比如下面的代码通过sample_perfect_tile来采样可能的tile size:
def stochastic_schedule_mm(s: tvm.tir.Schedule):
m, l, k = s.get_loops('C')
m_factors = s.sample_perfect_tile(loop=m, n=2)
mo, mi = s.split(m, m_factors)
k_factors = s.sample_perfect_tile(loop=k, n=2)
ko, ki = s.split(k, k_factors)
l_factors = s.sample_perfect_tile(loop=l, n=2)
lo, li = s.split(l, l_factors)
s.reorder(mo, lo, ko, mi, ki, li)
return s可以多次执行下面这段代码, 每次都会采样出一个随机的tile size, 在操作上可以采用多次实验然后保存下最优性能下的调度方式, 但因为过于耗时这里就不尝试了:
prim_func = te.create_prim_func([A, B, E, F])
tir_sch = tvm.tir.Schedule(prim_func)
tir_sch = stochastic_schedule_mm(tir_sch)
rt_lib = tvm.build(tir_sch.mod, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")
tir_sch.mod.show()Time cost of transformed sch.mod 5.9412203167 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
for m_0, l_0, rk_0, m_1, rk_1, l_1 in T.grid(128, 128, 512, 8, 4, 8):
with T.block("C"):
v_m = T.axis.spatial(1024, m_0 * 8 + m_1)
v_l = T.axis.spatial(1024, l_0 * 8 + l_1)
v_rk = T.axis.reduce(2048, rk_0 * 4 + rk_1)
T.reads(A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
with T.init():
C[v_m, v_l] = T.float32(0.0)
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m, l in T.grid(1024, 1024):
with T.block("D"):
v_m, v_l = T.axis.remap("SS", [m, l])
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for m, n, rl in T.grid(1024, 3072, 1024):
with T.block("F"):
v_m, v_n, v_rl = T.axis.remap("SSR", [m, n, rl])
T.reads(D[v_m, v_rl], E[v_rl, v_n])
T.writes(F[v_m, v_n])
with T.init():
F[v_m, v_n] = T.float32(0.0)
F[v_m, v_n] = F[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
Meta Schedule
在实践中, 需要使用更快速更智能的算法. tvm的meta schedule是支持搜索可能变换空间的命名空间, 他实现了如下功能
- 并行搜索
- 使用cost model来避免每次都进行benchmark
- 基于历史轨迹进行遗传搜索evolutionary search, 而不是每次都随机采样
尽管工具变了, 但关键思想是保持不变的: 使用随机变换在指定的程序搜索空间中找到最优的调度方式.
from tvm import meta_schedule as ms
# disable parallel when num cores = 1.
rules = ms.ScheduleRule.create('llvm')
newrules = []
for rule in rules:
if isinstance(rule, ms.schedule_rule.ParallelizeVectorizeUnroll):
newrules.append(ms.schedule_rule.ParallelizeVectorizeUnroll(-1, 64, [0, 16, 64, 512], True))
else:
newrules.append(rule.clone())
mutators = ms.Mutator.create('llvm')
newmutators = []
for m in mutators:
if isinstance(m, ms.mutator.MutateParallel):
newmutators.append(ms.mutator.MutateParallel(-1))
else:
newmutators.append(m.clone())
sg = ms.space_generator.PostOrderApply(sch_rules=newrules)
database = ms.tune_tir(
mod=prim_func,
target="llvm --num-cores=1",
max_trials_global=64,
num_trials_per_iter=64,
work_dir="./tune_tmp",
num_tuning_cores=4,
space=sg,
)
sch = ms.tir_integration.compile_tir(database, prim_func, "llvm --num-cores=1")2024-08-08 15:05:06 [INFO] Logging directory: ./tune_tmp/logs
2024-08-08 15:05:06 [INFO] LocalBuilder: max_workers = 4
2024-08-08 15:05:06 [INFO] LocalRunner: max_workers = 1
2024-08-08 15:05:07 [INFO] [task_scheduler.cc:159] Initializing Task #0: "main"| Name | FLOP | Weight | Speed (GFLOPS) | Latency (us) | Weighted Latency (us) | Trials | Done | |
|---|---|---|---|---|---|---|---|---|
| 0 | main | 10737418240 | 1 | N/A | N/A | N/A | 0 |
2024-08-08 15:05:07 [DEBUG] [task_scheduler.cc:318]
ID | Name | FLOP | Weight | Speed (GFLOPS) | Latency (us) | Weighted Latency (us) | Trials | Done
----------------------------------------------------------------------------------------------------------
0 | main | 10737418240 | 1 | N/A | N/A | N/A | 0 |
----------------------------------------------------------------------------------------------------------
Total trials: 0
Total latency (us): 0
Total trials: 0
Total latency (us): 0
2024-08-08 15:05:07 [INFO] [task_scheduler.cc:180] TaskScheduler picks Task #0: "main"
2024-08-08 15:05:11 [INFO] [task_scheduler.cc:193] Sending 64 sample(s) to builder
2024-08-08 15:05:27 [INFO] [task_scheduler.cc:195] Sending 64 sample(s) to runner
2024-08-08 15:09:35 [DEBUG] XGB iter 0: tr-p-rmse: 0.549968 tr-a-peak@32: 0.877909 tr-rmse: 0.348221 tr-rmse: 0.348221
2024-08-08 15:09:35 [DEBUG] XGB iter 25: tr-p-rmse: 0.070855 tr-a-peak@32: 1.000000 tr-rmse: 0.397401 tr-rmse: 0.397401
2024-08-08 15:09:35 [DEBUG] XGB iter 50: tr-p-rmse: 0.070855 tr-a-peak@32: 1.000000 tr-rmse: 0.397401 tr-rmse: 0.397401
2024-08-08 15:09:35 [DEBUG] XGB stopped. Best iteration: [14] tr-p-rmse:0.07086 tr-a-peak@32:1.00000 tr-rmse:0.39740 tr-rmse:0.39740
2024-08-08 15:09:35 [INFO] [task_scheduler.cc:237] [Updated] Task #0: "main"| Name | FLOP | Weight | Speed (GFLOPS) | Latency (us) | Weighted Latency (us) | Trials | Done | |
|---|---|---|---|---|---|---|---|---|
| 0 | main | 10737418240 | 1 | 64.5722 | 166285.3613 | 166285.3613 | 64 |
Total trials: 64
Total latency (us): 166285
2024-08-08 15:09:35 [DEBUG] [task_scheduler.cc:318]
ID | Name | FLOP | Weight | Speed (GFLOPS) | Latency (us) | Weighted Latency (us) | Trials | Done
----------------------------------------------------------------------------------------------------------
0 | main | 10737418240 | 1 | 64.5722 | 166285.3613 | 166285.3613 | 64 |
----------------------------------------------------------------------------------------------------------
Total trials: 64
Total latency (us): 166285
2024-08-08 15:09:35 [INFO] [task_scheduler.cc:260] Task #0 has finished. Remaining task(s): 0| Name | FLOP | Weight | Speed (GFLOPS) | Latency (us) | Weighted Latency (us) | Trials | Done | |
|---|---|---|---|---|---|---|---|---|
| 0 | main | 10737418240 | 1 | 64.5722 | 166285.3613 | 166285.3613 | 64 | Y |
Total trials: 64
Total latency (us): 166285
2024-08-08 15:09:35 [DEBUG] [task_scheduler.cc:318]
ID | Name | FLOP | Weight | Speed (GFLOPS) | Latency (us) | Weighted Latency (us) | Trials | Done
----------------------------------------------------------------------------------------------------------
0 | main | 10737418240 | 1 | 64.5722 | 166285.3613 | 166285.3613 | 64 | Y
----------------------------------------------------------------------------------------------------------
Total trials: 64
Total latency (us): 166285尝试执行一下自动搜索出的最终程序, 可以发现性能提升了非常多倍, 从7s到了0.16s:
rt_lib = tvm.build(sch.mod, target="llvm")
f_timer = rt_lib.time_evaluator("__tvm_main__", tvm.cpu())
print(f"Time cost of transformed sch.mod {f_timer(a_nd, b_nd, e_nd, f_nd).mean} sec")
sch.mod.show()Time cost of transformed sch.mod 0.16998505 sec# from tvm.script import ir as I
# from tvm.script import tir as T
@I.ir_module
class Module:
@T.prim_func
def main(A: T.Buffer((1024, 2048), "float32"), B: T.Buffer((2048, 1024), "float32"), E: T.Buffer((1024, 3072), "float32"), F: T.Buffer((1024, 3072), "float32")):
T.func_attr({"tir.noalias": T.bool(True)})
# with T.block("root"):
C = T.alloc_buffer((1024, 1024))
D = T.alloc_buffer((1024, 1024))
F_global = T.alloc_buffer((1024, 3072))
for m_0 in T.serial(32, annotations={"pragma_auto_unroll_max_step": 512, "pragma_unroll_explicit": 1}):
for l_0, m_1, l_1 in T.grid(2, 1, 32):
for m_2_init, l_2_init, m_3_init in T.grid(32, 2, 1):
for l_3_fused_init in T.vectorized(8):
with T.block("C_init"):
v_m = T.axis.spatial(1024, m_0 * 32 + m_1 * 32 + m_2_init + m_3_init)
v_l = T.axis.spatial(1024, l_0 * 512 + l_1 * 16 + l_2_init * 8 + l_3_fused_init)
T.reads()
T.writes(C[v_m, v_l])
T.block_attr({"meta_schedule.tiling_structure": "SSRSRS"})
C[v_m, v_l] = T.float32(0.0)
for rk_0, m_2, l_2, rk_1, m_3 in T.grid(128, 32, 2, 16, 1):
for l_3_fused in T.vectorized(8):
with T.block("C_update"):
v_m = T.axis.spatial(1024, m_0 * 32 + m_1 * 32 + m_2 + m_3)
v_l = T.axis.spatial(1024, l_0 * 512 + l_1 * 16 + l_2 * 8 + l_3_fused)
v_rk = T.axis.reduce(2048, rk_0 * 16 + rk_1)
T.reads(C[v_m, v_l], A[v_m, v_rk], B[v_rk, v_l])
T.writes(C[v_m, v_l])
T.block_attr({"meta_schedule.tiling_structure": "SSRSRS"})
C[v_m, v_l] = C[v_m, v_l] + A[v_m, v_rk] * B[v_rk, v_l]
for m_0 in T.serial(4, annotations={"pragma_auto_unroll_max_step": 512, "pragma_unroll_explicit": 1}):
for ax0, ax1 in T.grid(256, 1024):
with T.block("D"):
v_m = T.axis.spatial(1024, m_0 * 256 + ax0)
v_l = T.axis.spatial(1024, ax1)
T.reads(C[v_m, v_l])
T.writes(D[v_m, v_l])
D[v_m, v_l] = T.exp(C[v_m, v_l])
for n_0, m_1, n_1 in T.grid(1, 4, 16):
for m_2_init, n_2_init, m_3_init in T.grid(32, 6, 2):
for n_3_fused_init in T.vectorized(32):
with T.block("F_init"):
v_m = T.axis.spatial(1024, m_0 * 256 + m_1 * 64 + m_2_init * 2 + m_3_init)
v_n = T.axis.spatial(3072, n_0 * 3072 + n_1 * 192 + n_2_init * 32 + n_3_fused_init)
T.reads()
T.writes(F_global[v_m, v_n])
T.block_attr({"meta_schedule.tiling_structure": "SSRSRS"})
F_global[v_m, v_n] = T.float32(0.0)
for rl_0, m_2, n_2, rl_1, m_3 in T.grid(128, 32, 6, 8, 2):
for n_3_fused in T.vectorized(32):
with T.block("F_update"):
v_m = T.axis.spatial(1024, m_0 * 256 + m_1 * 64 + m_2 * 2 + m_3)
v_n = T.axis.spatial(3072, n_0 * 3072 + n_1 * 192 + n_2 * 32 + n_3_fused)
v_rl = T.axis.reduce(1024, rl_0 * 8 + rl_1)
T.reads(F_global[v_m, v_n], D[v_m, v_rl], E[v_rl, v_n])
T.writes(F_global[v_m, v_n])
T.block_attr({"meta_schedule.tiling_structure": "SSRSRS"})
F_global[v_m, v_n] = F_global[v_m, v_n] + D[v_m, v_rl] * E[v_rl, v_n]
for ax0, ax1 in T.grid(64, 192):
with T.block("F_global"):
v0 = T.axis.spatial(1024, m_0 * 256 + m_1 * 64 + ax0)
v1 = T.axis.spatial(3072, n_1 * 192 + ax1)
T.reads(F_global[v0, v1])
T.writes(F[v0, v1])
F[v0, v1] = F_global[v0, v1]
但是…, 如果我们使用预先手写好的高度优化的算子, 比如通过numpy来测试一下性能:
def numpy_fn(a, b, e, f):
c = np.matmul(a, b)
np.exp(c, out=c)
np.matmul(c, e, out=f)
def numpy_benchmark():
a_np = np.random.randn(M, K).astype(np.float32)
b_np = np.random.randn(K, L).astype(np.float32)
e_np = np.random.randn(L, N).astype(np.float32)
f_np = np.empty((M, N), np.float32)
times = 20
time = np.testing.measure('numpy_fn(a_np, b_np, e_np, f_np)', times)
print(f"Time cost of numpy {time/times} sec")
from threadpoolctl import threadpool_limits
with np.testing.suppress_warnings() as sup:
sup.filter(RuntimeWarning)
with threadpool_limits(limits=1, user_api=None):
numpy_benchmark()Time cost of numpy 0.10500000000000001 sec可以发现虽然没有任何的fusion, 但手写算子还是优于自动搜索的结果. 这其实就是体现了目前的自动搜索方法所存在的局限性, 高度优化的gemm库中为了减少加载A/B矩阵的cache miss会进行online packing的操作, 比如blis的论文中的gebp策略:

gebp策略的本质其实是fuse了pack(A),pack(B),matmul(Packed(A),Packed(B),C)这三个操作, 而tvm只专注于matmul(A,B,C)内部的变化策略, 所以他难以达到最优. 不过blis所提出的策略也只对支持simd指令的cpu有效, 对于dsa架构的tensor core来说, 就需要重新基于优化的原则来设计分块策略, 这是一个复杂的过程.
更多资料
- Optimizing Compilers Modern Architectures
- TensorIR: An Abstraction for Automatic Tensorized Program Optimization
- BLISlab: A Sandbox for Optimizing GEMM