最大最小聚类

我写的最大最小聚类.但是我写的时候只写了依据最小进行聚类 233

算法流程

1. 随机找一个点为第一个聚类中心
2. 找距离这个点最远的点为第二个聚类中心
3. 遍历所有的欧式距离,以其中较小的距离为准,如果这个距离大于第一第二聚类点的\(\theta\)倍,那么这个点就是新的聚类点.重复直到没有新的聚类点.
4. 分类即可

代码

import math
import matplotlib.pyplot as plt
import numpy as np


def createDataSet():
    """
    创建测试的数据集，里面的数值中具有连续值
    :return:
    """
    dataSet = [
        [0.697, 0.460], [0.774, 0.376], [0.634, 0.264],
        [0.608, 0.318], [0.556, 0.215],
        [0.403, 0.237], [0.481, 0.149], [0.437, 0.211],
        [0.666, 0.091], [0.243, 0.267],
        [0.245, 0.057], [0.343, 0.099], [0.639, 0.161],
        [0.657, 0.198], [0.360, 0.370],
        [0.593, 0.042], [0.719, 0.103], [0.359, 0.188],
        [0.339, 0.241], [0.282, 0.257],
        [0.748, 0.232], [0.714, 0.346], [0.483, 0.312],
        [0.478, 0.437], [0.525, 0.369],
        [0.751, 0.489], [0.532, 0.472], [0.473, 0.376],
        [0.725, 0.445], [0.446, 0.459],
    ]

    # 特征值列表

    labels = ['密度', '含糖率']

    # 特征对应的所有可能的情况
    labels_full = {}

    for i in range(len(labels)):
        labelList = [example[i] for example in dataSet]
        uniqueLabel = set(labelList)
        labels_full[labels[i]] = uniqueLabel

    return dataSet, labels, labels_full


# 计算两点之间的欧式距离
def one_one_dict(a: list, b: list)->float:
    return pow(a[0]-b[0], 2)+pow(a[1]-b[1], 2)


# 计算一个点与所有聚类中心的欧式距离
def one_n_dict(sample, centers: list)->np.ndarray:
    sample = np.array(sample)
    centers = np.array(centers)
    # 将sample复制k次 与 centers 矩阵维度相同
    samples = np.tile(sample, (centers.shape[0], 1))
    # print(samples)
    # 矩阵相减然后平方，对每一列求和　distances＝[1 x k]
    distances = np.power(samples - centers, 2).sum(axis=1)
    return distances


# 计算n个点到一个中心点的欧式距离
def n_one_dist(X, c):
    c = np.array(c, ndmin=2)
    c_s = np.tile(c, (X.shape[0], 1))
    # 利用矩阵乘法求出欧式距离矩阵
    distances = np.power(X-c_s, 2).sum(axis=1)
    return distances


class Maxmin(object):
    def __init__(self, x, theta):
        self.x = x
        self.centers = []  # 聚类中心矩阵
        self.theta = theta  # 生成新聚类中心可能性

    # 确定第一个聚类中心
    def init_center(self, cent=None):
        """
        cent=None 时 随机生成初始聚类中心 否则指定点
        """
        if cent == None:
            cent_index = np.random.choice(np.shape(self.x)[0])
        else:
            cent_index = cent
        self.centers.append(self.x[cent_index])

    # 确定第二个聚类中心
    def second_center(self):
        dists = n_one_dist(self.x, self.centers[0])
        cent_index = np.argmax(dists)
        self.centers.append(self.x[cent_index])

    # 计算各个样本与中心点的距离,返回距离矩阵
    def calc_dist(self)->np.ndarray:
        dists = np.zeros((self.x.shape[0], len(self.centers)))
        for i in range(self.x.shape[0]):
            dist = one_n_dict(self.x[i],  self.centers)
            # 选距离中心点小的距离作为结果
            dists[i] = dist
        return dists

    # 生成新的聚类中心,返回是否成功生成
    def new_center(self, dists: np.ndarray)->bool:
        # 按列取最小值
        dists = np.min(dists, axis=1)
        # 最大距离大于两个中心点之间的距离就生成新中心点
        # 这里加pow是因为我前面算距离都没有开平方
        if pow(max(dists), 0.5) >\
                self.theta*pow(one_one_dict(self.centers[0], self.centers[1]), 0.5):
            self.centers.append(self.x[np.argmax(dists)])
            return True
        else:
            return False

    # 当没有新的聚类中心之后,生成对应类别
    def make_ylabel(self, dists: np.ndarray)->list:
        index = np.argmin(dists, axis=1)
        return index

    def fit(self, cent=None):
        """
        cent=None 时 随机生成初始聚类中心 否则指定点
        """
        # 得到第一个聚类中心
        self.init_center(cent)
        # 得到第二个聚类中心
        self.second_center()
        # 迭代计算新的聚类中心
        distances = self.calc_dist()
        while self.new_center(distances) == True:
            distances = self.calc_dist()
        # 根据距离获得label
        return self.make_ylabel(distances)


if __name__ == "__main__":
    # 书上的例子
    data = [[0, 0], [3, 8], [2, 2], [1, 1], [5, 3],
            [4, 8], [6, 3], [5, 4], [6, 4], [7, 5]]
    data = np.array(data)
    mm = Maxmin(data, 0.5)
    y = mm.fit()
    plt.scatter(x=data[:, 0], y=data[:, 1], c=y)
    plt.show()

    # 西瓜书中的数据
    data, _, _ = createDataSet()
    data = np.array(data)
    mm1 = Maxmin(data, 0.5)
    y = mm1.fit()
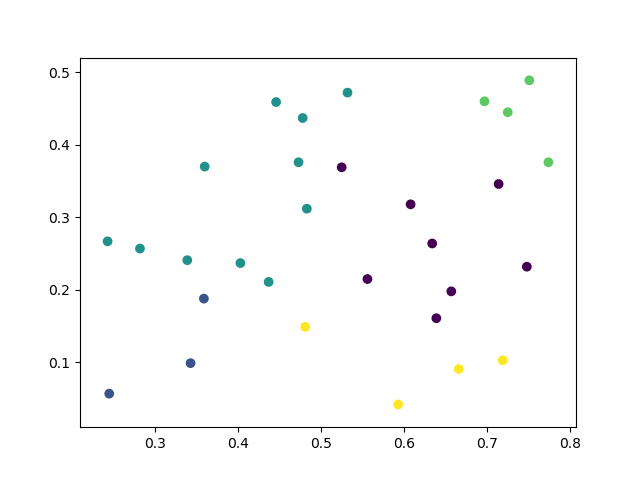
    plt.scatter(x=data[:, 0], y=data[:, 1], c=y)
    plt.show()

效果