统计学习方法:提升方法
提升方法。这个思路可以被考虑到集成中。提升方法AdaBoost的想法是将相同类型的不同参数的弱分类器的分类结果进行集成,他是一个串行的提升过程。此方法的流程比较清楚,关于原理部分建议大家仔细看书。
原理
他的方法是通过串行的训练:
- 提升弱分类器分类错误样本点的权重
- 提升准确率高的弱分类器输出结果权重
假设一个二类分类的训练数据集: \[\begin{aligned} D = \{\left( x_{1},y_{1} \right),\left( x_{2},y_{2} \right),\ldots,(x_{n},\ y_{n})\}\\ x_{i} \in X \subseteq \mathbb{R}^{n}\ ;y_{i} \in Y = \{ - 1,\ + 1\} \end{aligned} \]
开始训练,假设我们迭代\(M\)次,首先初始化权重分布\(W_k\)为均匀分布,对于\(k = 0,1,\ldots,\ M - 1\):
- 利用权重\(W_k\)训练弱分类器:
\[\begin{aligned} g_{k}(x):X \rightarrow \{ - 1,\ + 1\} \end{aligned} \]
- 计算分类器\(g_{k}(x)\)的加权错误率:
\[\begin{aligned} e_{k} = \sum_{i = 1}^{N}{w_{\text{k|i}}I(g_{k}\left( x_{i} \right) \neq y_{i})} \end{aligned} \]
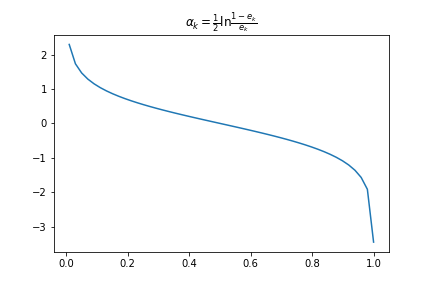
根据加权错误率计算分类器的输出结果权值: \[\begin{aligned} \alpha_{k} = \frac{1}{2}\ln\frac{1 - e_{k}}{e_{k}} \end{aligned} \]
根据分类器\(g_{k}(x)\)的错误率修改训练数据的权重,对于误分类的样本要增大权重,反之则减少。
\[ \begin{aligned} w_{k + 1,i} = \frac{w_{\text{k|i}}}{Z_{k}} \cdot exp( - \alpha_{k}y_{i}g_{k}(x_{i}))\\ Z_{k}=\sum_{i=1}^N w_{\text{k|i}} \cdot exp( - \alpha_{k}y_{i}g_{k}(x_{i})) \end{aligned} \]
- 重复以上过程,迭代结束后最终分类器如下:
\[ \begin{aligned} g\left( x \right) = \text{sign}\left( \sum_{k = 1}^{M}{\alpha_{k}g_{k}\left( x \right)} \right) \end{aligned} \]
题外话
错误率-权重映射关系: